Sabemos encontrar la raíz cuadrada de cualquier número real positivo. De manera similar, podemos encontrar la raíz cuadrada de un número negativo. La diferencia es que la raíz no es real. Si el valor del radicando es negativo, se dice que la raíz es un número imaginario. El número imaginario i se define como la raíz cuadrada de 1 negativo.
Así que, usando las propiedades de los radicales,
Podemos escribir la raíz cuadrada de cualquier número negativo como un múltiplo de i. Consideremos la raíz cuadrada de -25.
Usamos 5i y no -\text{5}i\\ porque la raíz principal de 25 es la raíz positiva.
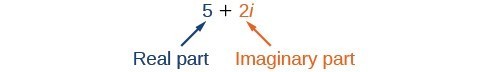
Figura 1
Un número complejo es la suma de un número real y un número imaginario. Un número complejo se expresa en forma estándar cuando se escribe a + bi donde a es la parte real y bi es la parte imaginaria. Por ejemplo, 5+2i\\\Nes un número complejo. También lo es 3+4\i\i.
Los números imaginarios se distinguen de los reales porque un número imaginario elevado al cuadrado produce un número real negativo. Recordemos que cuando un número real positivo se eleva al cuadrado, el resultado es un número real positivo y cuando un número real negativo se eleva al cuadrado, de nuevo, el resultado es un número real positivo. Los números complejos son una combinación de números reales e imaginarios.
Nota General: Números Imaginarios y Complejos
Un número complejo es un número de la forma a+bi\\\ donde
- a es la parte real del número complejo.
- bi es la parte imaginaria del número complejo.
Si b=0\\\\N, entonces a+bi\\Nes un número real. Si a=0\\ y b no es igual a 0, el número complejo se llama número imaginario. Un número imaginario es una raíz par de un número negativo.
Cómo: Dado un número imaginario, exprésalo en forma estándar.
- Escribimos \Nsqrt{a}\Ncomo \Nsqrt{a}\N-1}\N.
- Expresamos \Nsqrt{a}\Ncomo i.
- Escribimos \Nsqrt{a}\Ncdot i\Nen la forma más sencilla.
Ejemplo 1: Expresar un número imaginario en forma estándar
Expresar \sqrt{-9}\\a en forma estándar.
Solución
\aqrt{-9}=\aqrt{9}\aqrt{-1}=3i{11>
En forma estándar, esto es 0+3i{}.
Inténtalo 1
Expresa \sqrt{-24}\ en forma estándar.
Solución
