En esta sección, nos familiarizaremos con las operaciones y notaciones de los conjuntos, de modo que podamos aplicar estos conceptos tanto a problemas de conteo como de probabilidad. Comenzamos definiendo algunos términos.
Un conjunto es una colección de objetos, y sus miembros se llaman los elementos del conjunto. Nombramos el conjunto utilizando letras mayúsculas, y encerramos sus miembros entre corchetes. Supongamos que necesitamos enumerar los miembros del club de ajedrez. Usamos la siguiente notación de conjunto.
C ={Ken, Bob, Tran, Shanti, Eric}
Un conjunto que no tiene miembros se llama conjunto vacío. El conjunto vacío se denota con el símbolo Ø.
Dos conjuntos son iguales si tienen los mismos elementos.
Un conjunto A es subconjunto de un conjunto B si todo miembro de A es también miembro de B.
Supongamos que C = {Al, Bob, Chris, David, Ed} y A = {Bob, David}. Entonces A es un subconjunto de C, que se escribe como 
.
Todo conjunto es un subconjunto de sí mismo, y el conjunto vacío es un subconjunto de todo conjunto.
Unión de dos conjuntos
Siendo A y B dos conjuntos, entonces la unión de A y B, que se escribe como 
, es el conjunto de todos los elementos que están o en A o en B, o en ambos A y B.
Intersección De Dos Conjuntos
Siendo A y B dos conjuntos, entonces la intersección de A y B, escrita como 
, es el conjunto de todos los elementos que son comunes a ambos conjuntos A y B.
Un conjunto universal U es el conjunto formado por todos los elementos considerados.
Complemento de un conjunto
Siendo A un conjunto cualquiera, entonces el complemento del conjunto A, escrito como 
, es el conjunto formado por los elementos del conjunto universal U que no están en A.
Conjuntos disjuntos
Dos conjuntos A y B se llaman conjuntos disjuntos si su intersección es un conjunto vacío.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {naranja, verde, añil, violeta}Para lograr una mejor comprensión, supongamos que el conjunto universal U representa los colores del espectro, y P los colores primarios, entonces representa aquellos colores del espectro que no son primarios.
.
= {rojo, amarillo, azul, verde}
= {naranja, añil, violeta}
= {rojo, amarillo, azul, violeta} = {violeta}Diagramas de Venn
Ahora utilizamos los diagramas de Venn para ilustrar las relaciones entre conjuntos. A finales del siglo XIX, un lógico inglés llamado John Venn desarrolló un método para representar las relaciones entre conjuntos. Representó estas relaciones mediante diagramas, que ahora se conocen como diagramas de Venn. Un diagrama de Venn representa un conjunto como el interior de un círculo. A menudo, dos o más círculos están encerrados en un rectángulo donde el rectángulo representa el conjunto universal. Visualizar una intersección o unión de un conjunto es fácil. En esta sección, utilizaremos principalmente los diagramas de Venn para ordenar varias poblaciones y contar objetos.
|
(a) |
(b) |
(c) |
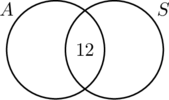
Porque 30 personas conducían coches con cambio automático, el círculo A debe contener 30 elementos. Esto significa que x + 12 = 30, o bien x = 18. Del mismo modo, como 20 personas conducían coches con transmisiones estándar, el círculo B debe contener 20 elementos, o y +12 = 20, lo que a su vez hace que y = 8.
Ahora que toda la información está ordenada, es fácil leer en el diagrama que 18 personas conducían coches con transmisiones automáticas solamente, 12 personas conducían ambos tipos de coches, y 8 conducían coches con transmisiones estándar solamente. Por lo tanto, 18 + 12 + 8 = 38 personas participaron en la encuesta.
|
(a) |
(b) |
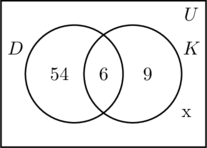
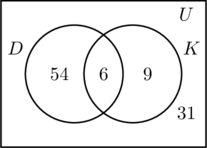
Rellenamos las tres regiones asociadas a los conjuntos D y K de la misma manera que antes. Dado que 100 personas participaron en la encuesta, el rectángulo que representa el conjunto universal U debe contener 100 objetos. Dejemos que x represente a las personas del conjunto universal que no están ni en el conjunto D ni en K. Esto significa que 54 + 6 + 9 + x = 100, o x = 31.
Por tanto, hay 31 personas en la encuesta que no han visitado ninguno de los dos lugares.
- 50 hacen footing, 30 nadan y 35 montan en bicicleta
- 14 hacen footing y nadan
- 7 nadan y montan en bicicleta
- 9 hacen footing y montan en bicicleta
- 3 personas participan en las tres actividades
Solución
|
(a) |
(b) |
(c) |
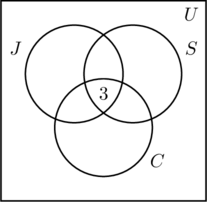
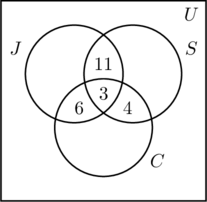
Colocamos un 3 en la región más interna de la figura (a) porque representa el número de personas que participan en las tres actividades. A continuación, calculamos x, y y z.
- Como 14 personas hacen footing y nadan, x +3 = 14, o sea, x = 11.
- El hecho de que 9 personas hagan footing y bicicleta da como resultado que y + 3 = 9, o bien y = 6.
- Como 7 personas nadan y montan en bicicleta, z + 3 = 7, o z = 4.
- Esta información se representa en la figura (b).
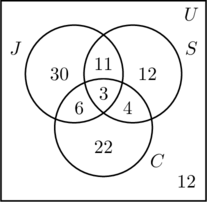
- Dado que 50 personas trotan, m + 11 + 6 + 3 = 50, o m = 30.
- 30 personas nadan, por lo tanto, n + 11 + 4 + 3 = 30, o n = 12.
- 35 personas montan en bicicleta, por lo tanto, p + 6 + 4 + 3 = 35, o p = 22.
- Al sumar todas las entradas de los tres conjuntos, obtenemos una suma de 88. Como se encuestó a 100 personas, el número que está dentro del conjunto universal pero fuera de los tres conjuntos es 100 – 88, o 12.
- En la figura (c), la información está ordenada, y las preguntas pueden responderse fácilmente.
Preguntas prácticas
1. Sea el conjunto universal U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h}, y W = {a, c, e, g, i}. Enumera los miembros de los siguientes conjuntos:
a. 
b. 
2. Considere los siguientes conjuntos: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, Gripe, Norovirus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella}, y C = {SARS, Listeria, Tuberculosis, H5N1, Salmonella, VIH, COVID-19}. Enumere los miembros de los siguientes conjuntos:
a. 
b. 
3. Una encuesta de atletas reveló que para sus dolores menores, 30 usaban aspirina, 50 usaban ibuprofeno y 15 usaban ambos. Todos los atletas encuestados utilizaban al menos uno de los dos analgésicos. ¿Cuántos atletas fueron encuestados?
4. Un estudio de 150 estudiantes de secundaria descubrió que 25 informaron de haber sufrido una conmoción cerebral o una lesión en la cabeza, 52 informaron de haber padecido una enfermedad mental y 15 informaron de ambos resultados. ¿Cuántos estudiantes no informaron de ninguno de los dos resultados?
5. Una encuesta realizada a 100 estudiantes de la Universidad Ryerson revela que 50 están suscritos a Netflix, 40 a Amazon Prime y 30 a Disney+. De ellos, 15 están suscritos tanto a Netflix como a Amazon Prime, 10 tanto a Amazon Prime como a Disney+, 10 tanto a Netflix como a Disney+, y 5 tienen los tres servicios de suscripción. Dibuja un diagrama de Venn y determina lo siguiente:
a. El número de estudiantes suscritos a Amazon Prime pero no a los otros dos servicios de streaming.
b. El número de estudiantes suscritos a Netflix o Amazon Prime pero no a Disney+.
c. El número de estudiantes que no están suscritos a ninguno de estos servicios.