
サモスのピタゴラス(570頃-495年)。 前8023>
Biography – Who was Pythagoras
純粋数学はピタゴラスに負うと主張され、彼はしばしば最初の「真の」数学者と呼ばれている。 しかし、彼の貢献が重要であることは明らかであるが、それにもかかわらず、彼は依然として論争の的となっている。
彼自身は数学的著作を残しておらず、ピタゴラス思想について我々が知っているものの多くは、フィロラオスや他の後代のピタゴラス学者の著作から得られている。
紀元前530年頃、彼が南イタリアのクロトンで開いた学校は、かなり奇妙なピタゴラス学派の核となった。 ピタゴラスの思想は主に数学に支配されていたが、深い神秘主義的なものでもあり、ピタゴラスは彼の学校のメンバー全員に、彼の準宗教的な哲学、厳しい菜食主義、共同生活、秘密の儀式、奇妙な規則(太陽に向かって排尿しない、金の宝石をつけている女性と結婚しない、道に横たわる驢馬を通り過ぎない、黒い空豆は食べることも触れることさえしないなど、奇妙で明らかに無作為な戒律を含む)を課した。
メンバーは、ピタゴラス自身が始めたより数学的・科学的な研究を拡張・発展させる「数学者」(または「学習者」)と、彼の教えのより宗教的・儀式的な側面に焦点を当てた「聴者」(または「聴取者」)に分けられた。 この2つのグループの間には常に一定の摩擦があり、やがて宗派は地元の激しい争いに巻き込まれ、最終的には分散してしまった。 ピタゴラス学派の秘密主義と排他性に対する憤りが高まり、紀元前460年、彼らの集会所はすべて焼かれ破壊され、クロトンだけでも少なくとも50人のメンバーが殺された
ピタゴラス学派の最大の教義は「すべては数」あるいは「神は数」であり、ピタゴラスは一種の数論あるいは数崇拝を実践し、それぞれの数は独自の性格と意味を持っていると考えた。 例えば、1という数字はすべての数字の発生源であり、2は意見、3は調和、4は正義、5は結婚、6は創造、7は7つの惑星または「さまよえる星」などを表していた。 8023>
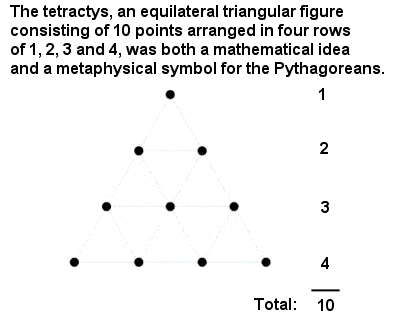
ピタゴラスのテトラキス
最も神聖な数は、1、2、3、4の和からなる三角形の数「テトラキス」または10であった。 ピタゴラスとその一派は、古代ギリシャの他の数学者と同様に、公理と論理を用いて第一原理から構築する、それまでよりも厳密な数学を導入することに大きく貢献したのである。 たとえば、ピタゴラス以前は、幾何学は経験的な測定によって導き出された規則の集まりにすぎなかった。
ピタゴラスは、幾何学的要素が数に対応し、整数とその比が論理と真理のシステム全体を構築するのに必要なものである、完全な数学体系が構築できることを発見したのである。
ピタゴラスの定理
彼は、ピタゴラスの定理(またはピタゴラスの定理)として知られるようになったことで主に記憶されている:任意の直角三角形について、斜辺(直角と反対の最も長い辺)の長さの二乗は、他の2辺(または「脚」)の二乗の和に等しいというものだ。
方程式で書くと、a2 + b2 = c2。
ピタゴラスとその信奉者が気づかなかったのは、これがどんな形にも当てはまるということである。したがって、斜辺の五角形の面積は、半円や他の正方形(あるいは不定形)のように、他の2辺の五角形の合計に等しくなる。
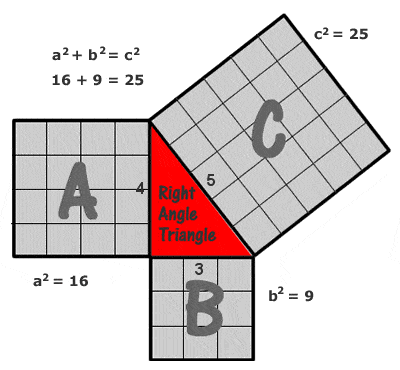
ピタゴラスの定理
ピタゴラスの三角形の最も簡単でよく引用される例は、3、4、5単位の辺(32 + 42 = 52.)を持つものである。 右図のように各辺に単位正方形のグリッドを描くとわかる)しかし、他にも(5、12、13)に始まり、(6、8、10)、(7、24、25)、(8、15、17)、(9、40、41)など、整数の「ピタゴラスの三角形」は無数にある可能性を秘めています。 ただし、(6, 8, 10) は (3, 4, 5) の倍数に過ぎないので、いわゆる「原始的な」ピタゴラス三角錐ではないことに注意しなければならない。
ピタゴラスの定理と直角三角形の性質は、基本的な算術と幾何学の次に古く、広く普及している数学的発展だと思われるが、1000年以上前のバビロンとエジプトの最も古い数学書のいくつかでこのことに触れられている。 最も単純な証明の一つは古代中国に由来し、おそらくピタゴラスの生誕よりかなり前のものであろう。 しかし、この定理に決定的な形を与えたのはピタゴラスである。ピタゴラス自身が決定的に証明したのか、単に記述しただけなのかは定かではない。 いずれにせよ、この定理は数学の定理の中で最もよく知られたものの1つとなり、現在では幾何学的、代数学的、高度な微分方程式などを含む400もの異なる証明が存在している
しかし、非整数の解も可能であることが徐々に明らかになり、たとえば、1、1、√2の辺を持つ2等辺三角形も直角を持つことが、バビロン人が数世紀前に発見したように、明らかになってきた。 しかし、ピタゴラスの弟子ヒッパソスが√2の値を計算しようとしたところ、分数で表せないことがわかり、新しい数の世界、無理数(整数の単純な分数で表せない数)の存在の可能性が示されたのである。 この発見は、ピタゴラスとその信奉者が築き上げた優雅な数学的世界をむしろ粉々にし、神の創造物である2つの比として表現できない数(彼らはこれを整数と考えた)の存在は、教団の信仰体系全体を危険にさらした。
哀れなヒッパソスは、この重要な発見を外の世界に伝えたために秘密主義のピタゴラスに溺死させられたようだ。 しかし、整数の神性という考え方が、より豊かな連続体の概念に置き換わったことは、数学の本質的な発展であった。 それは、線、面、角度を扱うギリシャ幾何学の真の誕生を意味した。
幾何学の他の業績として、ピタゴラス(あるいは少なくとも彼の信奉者であるピタゴラス人)は、三角形の角の和が2つの直角(180°)に等しいこと、またおそらく、n個の辺を持つ多角形の内角の和が(2n-4)個の直角に等しく、その外角の和が4個の直角に等しいという一般化も実現した。 8023>
ピタゴラスはまた、三角数、平方数、完全数(除数の和となる数)の研究により、整数論の基礎を確立した。 例えば、ある数nの2乗は最初の奇数n個の和に等しい(例:42=16=1+3+5+7)等、平方数の新しい性質をいくつか発見した。 例えば、220の約数は1、2、4、5、10、11、20、22、44、55、110で、その和は284であり、284の約数は1、2、4、71、142で、その和は220であった)。
音楽理論
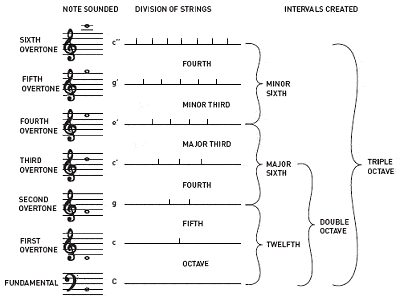
ピタゴラスは、調和のとれた音間の比率を発見したとされる
またピタゴラスは、調和のとれた音間の間隔は常に整数比であることを発見したとされる
。 例えば、ギターの弦を半分の長さで弾くと開放弦と同じ音になるが、オクターブ高くなる、3分の1の長さで弾くと異なるが調和のとれた音になる、など。 このように、ピタゴラスは、音楽のハーモニーの主要な構成要素となった共通の音程、すなわちオクターブ(1:1)、完全5度(3:2)、完全4度(4:3)、長3度(5:4)を作り出す最初の4つの倍音について説明したのです。
神秘主義者のピタゴラスはこの発見に興奮し、宇宙全体が数に基づいており、惑星や星は音符に対応する数式に従って動いていると確信し、一種のシンフォニー、「音楽的普遍性」または「球の音楽」を生み出しました。
| << ギリシャ数学に戻る | プラトンに進む > |
