私たちは、任意の正の実数の平方根を求める方法を知っています。 同じように、負の数の平方根を求めることができる。 違いは、根が実数でないことです。 半径の値が負の場合、根は虚数であると言われます。 虚数iは負の1の平方根と定義される。
そこで、ラジカルの性質を利用して、
任意の負数の平方根は、iの倍数と書くことができる。 \sqrt{-25}=25sqrt{25cdot \left(-1}right)}hill \text{ }=5i }hill \end{cases}
We use 5i and not -᷅ text{5}i } because the principal root of 25 is the positive root.
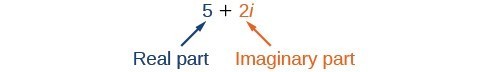
Figure 1
複素数とは、実数と虚数の和である。 複素数はa+biと書くと標準形で表され、aは実数部、biは虚数部である。 例えば、5+2iは複素数である。 3+4sqrt{3}i}もそうです。
虚数は2乗すると負の実数になるので、実数とは区別されます。 正の実数を2乗すると正の実数になり、負の実数を2乗するとまた正の実数になることを思い出してください。
A General Note: Imaginary and Complex Numbers
A complex number is a+bi 103 where
- a is the real part of the complex number.
- bi is the imaginary part of the complex number.
If b=0 001, then a+bi 001 is a real number.If b=0 001, then b=0 001, and bi 001 is a+bi 001 is a real number. a=0 Ⓐでbが0でない場合、その複素数は虚数と呼ばれます。 虚数は負の数の偶根である。
How To: 与えられた虚数を標準形式で表しなさい。
- Write \sqrt{-a} as \sqrt{-1}\.
- Express \sqrt{-1}\ as i.
- Write \sqrt{a}\cdot iếtliness in simplest form.これは虚数を簡単な形で表します。
Example 1: Expressing an Imaginary Number in Standard Form
Express \sqrt{-9}
(標準形).
解答
◇sqrt{-9}=◇sqrt{-1}=◇3i◇
標準形では0+3i◇である。
Try It 1
Express \sqrt{-24}\ in standard form.
Solution
