別名:評価者間信頼性またはコンコーダンス
統計学では、評価者間信頼性、評価者間一致、またはコンコーダンスは評価者間の一致度合いを表します。 1611>
ここで取り上げたKappasは「名目」データに最も適している。 データ中の自然な順序は(もし存在すれば)これらの方法では無視される。 もしこれらの測定基準を使用するのであれば、その制限を認識していることを確認すること。
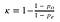
これには二つの部分がある。
- 観察された一致度を計算する
- 偶然の一致度を計算する
例えば、「はい」「いいえ」の回答、2人の評価者を扱うとします。 ここに評価があります。
rater1 =
rater2 =
この評価を混同行列にすると、

Observed agreement = (6 + 1) / 10 = 0.7
Chance agreement = probability of randomly saying yes (P_yes) + probability of randomly saying no (P_no)
P_yes = (6 + 1) / 10 * (6 + 1) / 10 = 0.49
P_no = (1 + 1) / 10 * (1 + 1) / 10 = 0.04
Chance agreement = 0.49 + 0.04 = 0.53
観察された一致は偶然の一致より大きいので正のカッパとなります。
kappa = 1 - (1 - 0.7) / (1 - 0.53) = 0.36
もしくは、sklearnの実装
from sklearn.metrics import cohen_kappa_scorecohen_kappa_score(rater1, rater2)
を使うと0.35714が返ってきますよ。
Kappaの解釈

特別な場合
Less than chance agreement
rater1 =
rater2 =
cohen_kappa_score(rater1, rater2)
-0.2121
If all
この場合、kappaは確実に0
rater1 = * 10
rater2 = * 10
cohen_kappa_score(rater1, rater2)
0.0
ランダム評価
ランダム評価の場合、Kappaは正規分布に従い、平均はほぼ0である。
評価数が増えると、分布の中のKappaの値のばらつきが小さくなる。
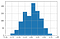
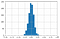
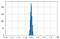
詳細はこちら
なお、コーエンカッパは2人の評価者が全く同じ項目を評価する場合のみ適用されます。
