群

群とは、有限または無限の要素集合と二項演算（群演算という）が一緒になって、閉鎖性、連想性、同一性、逆特性の4つの基本的性質を満たすものである。 群を定義する演算はしばしば「群演算」と呼ばれ、集合はこの演算の「下」で群であると言われる。 、、、…で、との間の二項演算をとすると、

1 のときに群を形成する。 閉包： とがの2要素なら、積のはにもある。

2. Associativity(連想性)。 定義された乗算は連想性、すなわちすべての, について。

3. 同一性。 すべての要素に対してとなるような同一要素（別名1、、）が存在する。

4.逆元。 各要素には逆数(incipals)があるはずである。 したがって、の各要素に対して、のような要素が集合に含まれる。

群は各要素が反転するモノイドである。

群は少なくとも1つの要素を含まなければならず、唯一の（同型までの）単一要素群はトリビアル群として知られる。 要素の数が有限である場合、その群は有限群と呼ばれ、要素の数は群の群順と呼ばれる。 群演算と逆演算のもとで閉じている群の部分集合を部分群と呼ぶ。 有限群の基本的な例は対称群で、これは個のオブジェクトの並べ換えの群（または「並べ換えの下」）である。 最も簡単な無限群は通常の足し算のもとでの整数の集合である。 連続群としては、実数や個の可逆行列の集合を考えることができる。

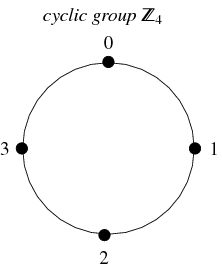
群の非常に一般的なタイプの1つは環状群である。 この群は整数の群（モジュロ）と同型で、、、と表記され、すべての整数に対して定義されている。 これは足し算で閉じており、連想的であり、一意な逆数を持つ。 0からまでの数はその要素を表し、恒等式を0、の逆数をで表す。

二つの群の間で恒等式と群演算を保存する写像を同型写像とよぶ。 同相が逆も同相である場合、それは同相と呼ばれ、2つの群は同型と呼ばれる。 互いに同型である2つの群は、抽象的な群として見た場合、「同じ」であるとみなされる。 例えば、下図に示す正方形の回転の群は巡回群.

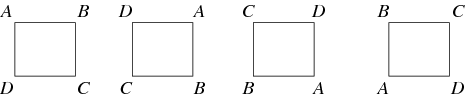
一般に群作用とは、ある群が集合に対してその要素を順列化して作用し、その群から集合の順列群への写像が同型になることである。 例えば、正方形の回転はその角の並べ換えの部分群となります。 任意の群の重要な群作用の1つは共役によるそれ自身への作用です。 これらは可能な群自動変形の一部に過ぎません。 群作用のもう一つの重要な種類は群表現で、群は可逆線形写像によってベクトル空間に作用する。 ベクトル空間の場が複素数の場合、表現は CG モジュールと呼ばれることもあります。

群作用、特に表現は群論だけでなく、物理や化学への応用でも非常に重要です。 群は抽象的な数学的対象として考えることができるので、同じ群が異なる文脈で生じることがある。 そのため、群の表現とは、群の1つの特殊な姿であり、他の表現を持つこともあると考えるのが便利である。 群の既約表現とは、表現行列をブロック対角形式に変換するユニタリー変換が存在しない表現である。 既約表現は、群直交性定理

で定式化されたように、多くの顕著な性質を持っている。