学習目標
このセクションの終わりまでに、次のことができるようになります:
- 典型的な光電効果実験について説明します。
- 別のエネルギーまたは波長の光子の最大運動エネルギーが与えられたとき、あるエネルギーまたは波長の光子によって放出される光電子の最大運動エネルギーを決定することができる
光が物質に当たると、物質から電子を放出することができます。 これを光電効果といい、光(フォト)が電気を発生させることを意味します。 光電効果の一般的な利用例としては、各種カメラの自動絞りを調整するための光量計などがあります。 また、電卓の中に入っていたり、屋根の上や道路に設置されているのを見たことがあるかと思いますが、太陽電池も同じようなものです。 4478>

図1.光電効果で光を電気に変換し、さまざまな機器を動かす。 この真空管内の金属板に光を当てると、光電効果を観察することができる。 光によって飛び出した電子はコレクター線に集められ、電流として測定される。 このとき、コレクター線とプレート間の遅延電圧を調整し、放出される電子のエネルギーを決定することができる。 例えば、十分な負電圧をかけると、電子はワイヤーに到達しない。 (credit: P.P. Urone)
この効果は1世紀以上前から知られており、図1に示すような装置を使って研究することが可能である。 この図は、金属板とコレクタ線が可変電圧源で接続された真空管で、コレクタは金属板よりも負側にある。 真空管内のプレートに光(または他の電磁波)が当たると、電子が放出されることがある。 電子のエネルギーが電子ボルト(eV)で、プレートとワイヤーの電位差(ボルト)より大きい場合、いくつかの電子はワイヤーに集められる。 電子のエネルギーをeVで表すと、qは電子の電荷、Vは電位差なので、ワイヤーとプレートの間の遅延電圧を調整することで、電子のエネルギーを測定することができる。 電子がワイヤーに到達するのを阻止する電圧は、エネルギー(eV)に等しい。 例えば、-3.00Vでやっと電子を止めることができれば、そのエネルギーは3.00eVとなる。 ワイヤーとプレートの間に流れる電流を測定することで、飛び出した電子の数を知ることができる。 4478>
光電効果で本当に重要なことは、アインシュタインがそこから何を推論したかということです。 アインシュタインは、光電効果には、電磁波が量子化されている場合にのみ説明できるいくつかの特徴があることに気づきました:電磁波の一見連続したエネルギーの流れは、実は光子というエネルギー量子で構成されているのです。 アインシュタインは、光電効果の説明の中で、電磁波の周波数に比例したエネルギーを持つ、量子化された単位、すなわち現在光子と呼ばれるものを定義しました。 ここで、Eは周波数fの光子のエネルギー、hはプランク定数であり、光子のエネルギーは、E=hfとなる。 この画期的なアイデアは、プランクの黒体発振器におけるエネルギー状態の量子化に似ているが、全く異なるものである。 それは、電磁波の量子化そのものである。 EM波は光子から構成されており、これまでの光学の章で説明したような連続した滑らかな波ではありません。 そのエネルギーは塊で吸収され、放出されるのであって、連続的なものではありません。 これは、プランクによる黒体発振器のエネルギー準位の量子化と全く同じで、黒体発振器はE=hfの光子を吸収・放出することによってhfの単位でエネルギーを増減させるからである。 しかし、一般的な光源には多くの光子が存在するため、個々の光子の存在に気づかず、目で見ることはできない。 (図2参照)次の章(光子エネルギーと電磁波スペクトル)では、光子について、その特徴や意味について説明します。 4478>
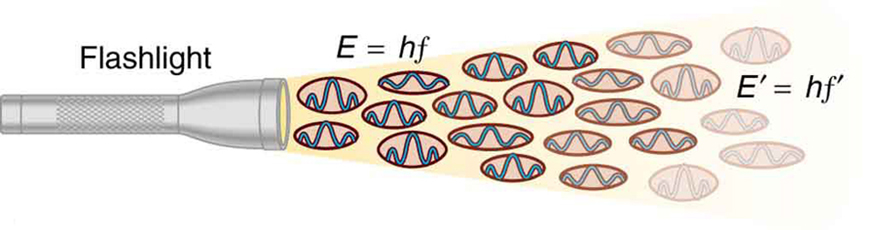
図2.光電効果を説明するために、アインシュタインが行ったように、今のところは光子の概念を使って説明します。 周波数fの電磁波は、光子、すなわち電磁波の個々の量子から構成される。 各光子のエネルギーはE=hfであり、hはプランク定数、fはEM放射の周波数である。 強度が高いほど、単位面積あたりの光子の数が多いことを意味します。 懐中電灯は多くの異なる周波数の光子を放出するので、他の光子はエネルギーE′=hf′を持ち、以下同様となります。 これらの性質はすべて、EM放射の個々の光子が物質中の個々の電子に吸収され、電子が光子のエネルギーを獲得するという考えと一致する。 これらの特性の中には、EM放射が単純な波であるという考えと矛盾するものもある。 簡単のために、すべての光子が同じエネルギーhfを持つ単色電磁放射で何が起こるかを考えてみましょう。
- ある物質に降り注ぐ電磁放射の周波数を変化させると、次のことがわかります。 ある物質では、EM放射の周波数f0以下では強度に関係なく電子が放出されない閾値が存在する。 個々の光子は個々の電子と相互作用する。 したがって、光子のエネルギーが小さすぎて電子を分解できない場合は、電子が放出されることはない。 もし電磁波が単純な波であれば、強度を大きくすれば十分なエネルギーが得られるが、
- 電磁波が物質に降り注ぐと、電子は遅滞なく放出される。 十分に高い周波数の個々の光子が個々の電子に吸収されると同時に、その電子は放出される。 もし電磁波が単純な波であれば、電子を放出するのに十分なエネルギーが金属表面に降り注ぐのに数分かかる。
- 単位時間あたりに放出される電子の数は、電磁波の強度に比例し、それ以外の特性はない。 高強度のEM放射は単位面積あたり大量の光子からなり、すべての光子は同じ特性エネルギーhfを持っている。
- EM放射の強度を変え、放出された電子のエネルギーを測定すると、次のことがわかる。 放出された電子の最大運動エネルギーは電磁波の強度に依存しない。 物質中には非常に多くの電子が存在するので、2つの光子が同時に同じ電子と相互作用して、その電子に与えるエネルギーを増大させることは極めてまれである。 その代わり(上記3で述べたように)、強度が増すと、同じエネルギーの電子がより多く放出されることになる。
- 放出される電子の運動エネルギーは、光子のエネルギーから特定の物質における電子の結合エネルギーを引いたものに等しい。 個々の光子はそのエネルギーのすべてを電子に与えることができる。 光子のエネルギーの一部は、電子を物質から引き離すために使われます。 残りのエネルギーは、放出された電子の運動エネルギーとして使われます。 ここで、KEeは放出される電子の最大運動エネルギー、hfは光子のエネルギー、BEは電子の特定の物質に対する結合エネルギーであり、式で表すと、KEe=hf-BEとなる。 (この式は1905年にアインシュタインが発表したもので、光電効果の性質を定量的に説明するものである。 EM放射の個々の光子(それ以外の方法で来ることはない)は、個々の電子と相互作用し、電子を破壊するのに十分なエネルギーBEを供給し、残りは運動エネルギーになる。 結合エネルギーはBE=hf0であり、f0は特定の物質に対する閾値周波数である。 図3は、ある物質に入射する電磁波の周波数に対する最大KEeのグラフである
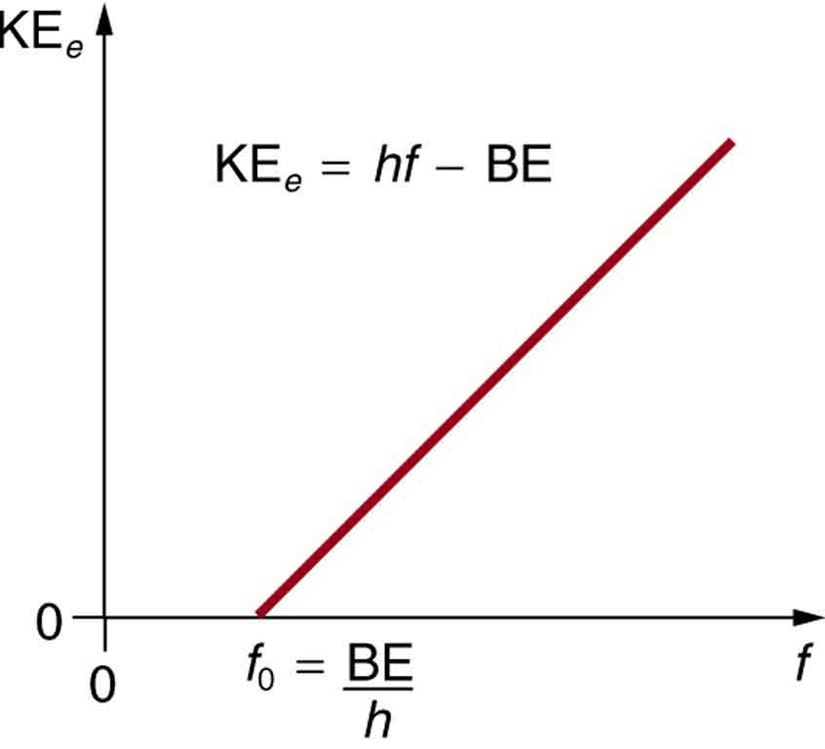
図3. 光電効果。 放出される電子の運動エネルギーKEeと、ある物質に降り注ぐ電磁波の周波数とのグラフ。 電子と相互作用する光子のエネルギーが不足し、電子が放出されない閾値周波数が存在する。 閾値エネルギー以上では、KEeはfに対して直線的に増加し、KEe=hf – BEと一致する。 この直線の傾きはhであり、このデータからプランク定数を実験的に求めることができる。
電磁放射が量子化されるというアインシュタインの考えは、量子力学の始まりに重要な意味を持ちました。 それは、光電効果の説明から想像されるよりもはるかに一般的な概念である。 EM放射はすべて光子の形でモデル化することができ、EM放射の特性はこの事実と完全に一致している。 (次節で述べるように、紫外線の危険性など、電磁波の多くの側面は光子の性質によってのみ説明できる)。 現代相対性理論で有名なアインシュタインは、1905年、特殊相対性理論の最初の論文を発表したのと同じ年に、量子力学の重要な種をまいている。 光電効果の説明は、1921年のノーベル賞受賞の基礎となった。 理論物理学への他の貢献もその受賞で注目されたが、特殊相対性理論と一般相対性理論は、1921年までに実験によって部分的に検証されていたにもかかわらず、十分な評価を受けることはなかった。 英雄視されながら、この偉大な人物は、彼の最も有名な仕事である相対性理論でノーベル賞を受けることはなかったのです。 光子のエネルギーと光電効果の計算。 紫色の光
1. 420nmの紫色光の光子のエネルギーはジュール、電子ボルトで何ボルトか?
2. 金属カルシウムに対する電子の結合エネルギー(または仕事関数)が2.71eVであるとき、420nmの紫色光でカルシウムから飛び出す電子の最大運動エネルギーは何ボルトか?
Strategy
その1、を解くために、光子のエネルギーはE = hfで与えられることに注目してください。 Part2については、光子のエネルギーが計算できれば、BEが与えられるので、KEe = hf – BEをそのまま適用して、放出される電子の最大運動エネルギーを求めることができます。
Part1の解答
光子のエネルギーはE = hfで与えられることがわかります。
周波数ではなく波長が与えられているので、周波数についておなじみの関係c = fλを解くと、f=frac{c}{lambda}}となります。
この二つの式を組み合わせると、E=frac{hc}{lambda}という便利な関係式が得られます。
ここで既知の値を代入すると
Thisdisplaystyle{E}=Centafrac{left(6.63Times10^{-34}text{ J}Cdot Text{ s}right)\left(3.63Times10^{-34}Tentafrac{ J}Cdot Text{ s}) となりまっせ。00times10^{8} text{ m/s}right)}{420times10^{-9} text{ m}}=4.74Times10^{-19} text{ J}
eVに変換すると、光子のエネルギーは
displaystyle=E}displaystyle(4.47times10^{-19} text{ J}right)\frac{1}text{ eV}}{1.6times10^{-19} text{ J}}=2.96}text{ eV}
Solution for Part 2
飛び出した電子の運動エネルギーは KEe = hf – BE という方程式で簡単に求めることができるようになりました。 光子エネルギーと結合エネルギーを代入すると、KEe = hf – BE = 2.96 eV – 2.71 eV = 0.246 eVとなる。
考察
この420nmの紫光のエネルギーは1ジュールのごく一部なので、光子1つを人間が直接感じることが難しいのは不思議なことではない-人間はジュール単位のエネルギーにより敏感である。 しかし、電子ボルトという単位で見てみると、この光子は原子や分子に影響を与えるのに十分なエネルギーを持っていることがわかります。 例えば、DNAは約1eVのエネルギーで切断され、原子や分子のエネルギーはeVのオーダーが一般的なので、今回の紫外線は生物学的な影響を与える可能性がある。 放出された電子(光電子と呼ばれる)のエネルギーはかなり低く、真空中を除いては遠くまで移動することはない。 電子は0.26eVの遅延電位で止まってしまう。 実は、もし光子の波長が長く、エネルギーが2.71eV以下であれば、この式は負の運動エネルギーを与えることになり、不可能なのである。 これは、2.96eVのエネルギーを持つ420nmの光子は、周波数の閾値をあまり超えていないことを意味している。 閾値の波長が459nm(青色光)であることは、自分で示すことができる。 つまり、金属カルシウムを光量計に用いると、青色光よりも長い波長には鈍感になる。 たとえば、赤色光にはまったく反応しません。
PhET Explorations: 光電効果
光がどのように金属製のターゲットから電子をたたき出すかを見て、量子力学の分野を生み出した実験を再現します。

シミュレーションをダウンロードするにはクリックしてください。 Java を使用して実行します。
Section Summary
- 光電効果とは、EM放射が物質から電子を放出するプロセスです。
- アインシュタインは、光子とはエネルギーE=hf(fは放射の周波数)を持つEM放射の量子のことであると提案しました。 アインシュタインが説明したように、光電効果のすべての特性は、個々の光子と個々の電子の相互作用によるものである。
- 放出された電子(光電子)の最大運動エネルギーKEeは、KEe = hf – BEで与えられ、hfは光子エネルギー、BEは特定の物質に対する電子の結合エネルギー(または仕事関数)である。
Conceptual Questions
- 光電効果を引き起こすことができる電磁波は可視光だけですか?
- 光電効果のどの部分が光子なしでは説明できませんか? 光子なしでも説明できるのはどれですか。 後者は光子の存在と矛盾しますか。
- 光電効果はEM放射の波としての性質とEM放射の粒子としての性質のどちらから生じるのですか。 簡単に説明してください。
- 絶縁体(非金属)は金属よりもBEが高く、光子が絶縁体から電子を放出することは困難である。
- 電子が自由に動いている金属片を手に取って振っても、電子は落ちてきません。 それでも金属を加熱すれば、電子は沸騰することがあります。
問題 & 演習
- 結合エネルギーが4.73eVとすると、銀から光電子を放出できる最長波長の電磁波は何であるか? これは可視域でしょうか?
- 結合エネルギーが2.24eVであるとして、カリウムから電子を放出できる最長波長の光子を求めよ。 これは可視光線ですか。
- 電子を放出できる最長波長の光子が337nmの場合、マグネシウムの電子の結合エネルギーはeVで何ですか。
- 電子を放出できる最長波長の光子が304nmの場合、アルミニウムの電子の結合エネルギーをeVで計算しなさい。
- 450nmの電磁波でナトリウム金属から飛び出した電子の運動エネルギーは、結合エネルギーが2.28eVとするとeVで何倍になるか。
- 波長120nmの紫外線が金金属に当たり、電子は4.82eVで結合しています。 放出された光電子の最大運動エネルギーはいくらか。
- 波長400nmの紫光は、ナトリウム金属から最大運動エネルギー0.860eVの電子を放出する。
- 波長300nmの紫外線がウラン金属に降り注ぎ、0.500eVの電子が放出されます。
- (a) カルシウムの結合エネルギーが2.71eVであるとき、カルシウム金属から2.00eVの電子を放出させる電磁波の波長は? (b)これはどのような電磁波か。
- 結合エネルギーが2.24eVであるとき、カリウムから0.100eVの電子を放出する光子の波長を求めよ。
- 80nmの光子によって物質から放出される電子の最大速度は、電子が物質に4.73eVで結合している場合、どの程度ですか。
- 結合エネルギーが2.71eVの物質からの光電子は420nmの光子で放出されます。 放出された後、これらの電子は検出装置まで2.50cm移動するのに何分かかるか。
- 波長400nmで出力2.00mWのレーザーをカルシウム金属に照射した。 (a)1秒間に何個の電子が放出されるか。 (b)結合エネルギーが2.71eVであることから、電子が持ち去るパワーはどのくらいか。
- (a) 1.30kW/m2の強度の500nm電磁波(地球大気上空の太陽光の強さ)により金属ナトリウムから放出された光電子の数/sを計算しなさい。 (b) 結合エネルギーが2.28eVであるとき、電子はどの程度の電力を持ち去るだろうか? (c) 電子が持ち去る電力は、光子によってもたらされる電力よりも小さい。 残りの電力はどこへ行くのだろうか? どうすれば回収できるか?
- 不合理な結果。 波長700nmの赤色光を、電子が3.68eVで結合している金属マグネシウムに照射する。 (a) KEe = hf – BE を用いて、飛び出した電子の運動エネルギーを計算しなさい。 (b) この結果のどこが不合理か。 (c) どの仮定が不合理か、矛盾しているか。
- 不合理な結果。 (a) 400nmの電磁波で4.00eVの電子が飛び出す物質に対する電子の束縛エネルギーはどのくらいか? (b)この結果のどこが不合理か? (c)どの仮定が不合理または矛盾しているか?
用語解説
光電効果:ある物質に光を当てると電子が放出される現象
光子:電磁波の量子、または粒子
光子エネルギー:光子のエネルギー。 E = hf
結合エネルギー:仕事関数とも呼ばれ、物質から電子を放出するのに必要なエネルギー量
問題精選 &演習
1. 263 nm
3. 3.69 eV
5. 0.483 eV
7. 2.25 eV
9. (a) 264 nm、(b) 紫外線
11. 1.95 × 106 m/s
13. (a) 4.02 × 1015 s、(b) 0.256 mW
15. (a) -1.90 eV; (b) 負の運動エネルギー; (c) 電子が自由にたたき出されること
15.
