このセクションでは、集合操作と表記に慣れ、これらの概念を計数と確率の両方の問題に適用できるようにします。 まず、いくつかの用語を定義する。
集合はオブジェクトの集まりであり、そのメンバーを集合の要素と呼ぶ。 集合の名前は大文字で表し、そのメンバーを中括弧で囲む。 例えば、チェスクラブのメンバーをリストアップする必要があるとします。 9332>
C ={Ken, Bob, Tran, Shanti, Eric}
メンバのない集合は空集合と呼ばれます。 空集合は記号Øで示される。
二つの集合は同じ要素を持つとき等しい。
集合AはAのすべてのメンバーがBのメンバーでもあるとき集合Bの部分集合である。
C={アル、ボブ、クリス、デイビッド、エド}とA={ボブ、デイビッド}と仮定する。
すべての集合はそれ自身の部分集合であり、空集合はすべての集合の部分集合である。
Union Of Two Sets
AおよびBを二つの集合とすると、![]() と書かれるAとBの和はAかB、またはAおよびB両方に含まれるすべての要素の集合である。
と書かれるAとBの和はAかB、またはAおよびB両方に含まれるすべての要素の集合である。
Intersection Of Two Sets
AとBを二つの集合とすると、![]() と書くAとBの交差は、集合AとBの両方に共通するすべての要素の集合である
と書くAとBの交差は、集合AとBの両方に共通するすべての要素の集合である
普遍集合Uは考察対象のすべての要素から成る集合である
二つの集合の交差はAを含む集合とする。
集合の補集合
Aを任意の集合とすると、![]() と書かれる集合Aの補集合は、普遍集合Uの中でAに含まれない要素からなる集合である。
と書かれる集合Aの補集合は、普遍集合Uの中でAに含まれない要素からなる集合である。
不接合集合
二つの集合A、Bはその交点が空集合であれば不接合集合という。
空集合はあらゆる集合の部分集合であり、集合はそれ自身の部分集合であることに注意せよ。
![]() = {橙、緑、藍、紫}
= {橙、緑、藍、紫}
理解を深めるために、普遍集合Uがスペクトルの色、Pが原色だとすると、![]() は原色でないスペクトルの色を表していることになります。
は原色でないスペクトルの色を表していることになります。
Venn Diagrams
現在、集合間の関係を表すのにVenn Diagramを使用しています。 1800年代後半、イギリスの論理学者ジョン・ベンが集合間の関係を表現する方法を開発した。 彼は、これらの関係を図を使って表現し、それが現在ではベン図として知られています。 ベン図は、集合を円の内部として表現する。 多くの場合、2つ以上の円が長方形で囲まれ、その長方形が普遍集合を表している。 集合の交差点や和集合を視覚化するのは簡単である。 9332>
|
(a) |
(b) |
(c) |
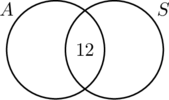
30人がAT車に乗っていたからである。 円Aは30個の要素を含んでいなければならない。 つまり、x+12=30、またはx=18となる。 同様に、20人が標準的なトランスミッションの車を運転したので、円Bには20個の要素が含まれなければならない。つまり、y +12 = 20で、y = 8となる。
すべての情報が整理されたので、図から、18人が自動変速機の車だけ、12人が両方の車、8人が標準変速機の車だけということが簡単に読み取れます。 したがって、18+12+8=38人が調査に参加したことになる。
|
(a) |
(b) |
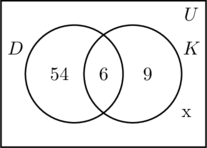
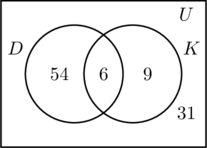
前と同じようにセットD、Kに関する三つの領域を埋めます。 アンケートに参加したのは100人なので、普遍集合Uを表す長方形には100個のオブジェクトが含まれるはずである。 xは普遍集合の中で集合DにもKにも入っていない人を表すとすると、54+6+9+x=100、つまりx=31です。
したがって、アンケートにはどちらの場所にも行っていない人が31人いることがわかります。
- ジョギング50人、水泳30人、自転車35人
- ジョギングと水泳14人
- 水泳と自転車7人
- ジョギングと自転車9人
- 3人が3つ全ての活動をしている
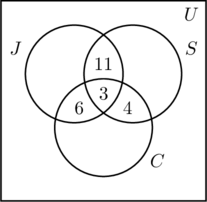
- 14人がジョギングと水泳をしているので、x+3=14、つまりx=11となる。
- 9人がジョギングとサイクリングをすることから、y+3=9、つまりy=6となる。
- 7人が水泳とサイクリングをしているので、z + 3 = 7、つまりz = 4となる。
- この情報を図(b)に示す。
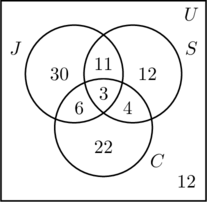
- 50人がジョギングするので、m+11+6+3=50、つまりm=30となる。
- 30人が泳ぐので、n + 11 + 4 + 3 = 30、またはn = 12。
- 35人が自転車で走るので、p + 6 + 4 + 3 = 35、またはp = 22。
- 3つのセットのすべての項目を足すと、合計が88になる。 100人を調査したので、普遍集合の中にあって3つの集合の外にある数は100-88、つまり12である。
- 図(c)では情報が整理され、質問に容易に答えられる。
解答
|
(a) |
(b) <1959> |
(c) <9332 |
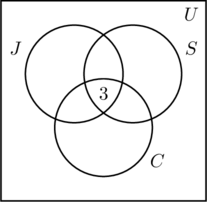
図(a)の一番内側の領域に3を置いたのは、3つの活動すべてに参加している人数を表すからである。 次にx、y、zを計算する。
練習問題
1. 普遍集合U={a,b,c,d,e,f,g,h,i,j},V={a,e,i,f,h},W={a,c,e,g,i}であるとする。 次の集合のメンバーを列挙せよ:
a. ![]()
b. ![]()
2.次の集合を考える。 A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, Influenza, Norovirus}、B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella}、C = {SARS, Listeria, Tuberculosis, H5N1, Salmonella, HIV, COVID-19} を考えてみよう。 次の集合のメンバーをリストアップする:
a. ![]()
b. ![]()
3. スポーツ選手を対象にした調査で、ちょっとした痛みにアスピリン30人、イブプロフェン50人、両方使う人は15人であることがわかった。 調査対象となったすべてのアスリートが、2つの鎮痛剤のうち少なくとも1つを使用していました。 調査対象となったアスリートは何人ですか? 9332>
4. 高校生150人を対象にした調査では、過去に脳震盪や頭部外傷を経験したと答えたのは25人、精神疾患を経験したと答えたのは52人、その両方を経験したと答えたのは15人でした。 どちらの結果も報告しなかった生徒は何人いますか?
5. ライアソン大学の学生100人を調査したところ、50人がNetflixに、40人がAmazon Primeに、30人がDisney+に加入していることがわかりました。 このうち、15人はNetflixとAmazon Primeの両方に、10人はAmazon PrimeとDisney+の両方に、10人はNetflixとDisney+の両方に、5人は3つのサブスクリプションサービスすべてに加入していることがわかった。 ベン図を描き、以下を判定する:
a. Amazonプライムに加入しているが、他の2つのストリーミングサービスに加入していない生徒の数
b. NetflixまたはAmazon Primeに加入しているが、Disney+には加入していない学生数。
c. いずれのサービスにも加入していない学生数.
c.