理科 > 物理学 > 光電効果 >アインシュタインの光電方程式
ここでは、アインシュタインの光電方程式を導出して、光の光電効果の特徴を確かめるために利用することを検討します。
光の波動性:
クリスチャン・ホイゲンは、光は波として伝搬すると提唱しました。 しかし、この理論には重大な欠点がある。 それは、真空中の光の伝播を説明することができなかったことである。 この欠点は、マクスウェルによって削除されました彼は光が電磁波であり、電磁波の伝播のための物質的な媒体は必要ありませんことを提案した。 このように、光の波動性が確立された。
波動理論は、光の伝播に関連するすべての現象を説明することができた。 しかし、エネルギー分布や光電効果、クロンプトン効果などの現代的な現象は説明できなかった。
光の粒子性:
Max Planckは、光やエネルギーの伝播は量子というエネルギーのパケットの形で行われることを証明した。 光の量子は光子と呼ばれ、こうして彼は光の粒子性を確立した。 プランクの量子論:
量子論は、マックス・プランクによって提唱されました。 この理論によると、光源からの放射は連続的に放出されるのではなく、エネルギーの束やパケットになって放出されます。 これらのパケットは量子あるいは光子と呼ばれる。 放射線が周波数νの場合、各量子はエネルギーを持ち、ここでhはプランク定数である。
したがって、光子のエネルギー=E=hν
エネルギーは不連続的に放出される。
電磁波の粒子性:
放射線と物質との相互作用において、放射線はあたかも粒子から成るかのように振舞う。 これらの粒子は光子と呼ばれる。 各フォトンは、
E = hν = hc/λ
特定の周波数(波長)の光のすべてのフォトンは、それらに関連付けられた同じ量のエネルギーを持っているで与えられるエネルギーを持っています。 光の強度が増すと、ある面積を通過する1秒あたりの光子の数は増えますが、各光子のエネルギーは同じになります。 フォトンは電気的に中性で、電界や磁界の影響を受けません。
各光子の運動量は
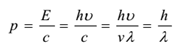
光子の波長は媒体によって変わるので、媒体によって異なる速度になる。 光子の静止質量は0である。 その運動質量は
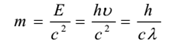
光子の粒子衝突(光子と電子の衝突など)では、全エネルギーと運動量は保存されます。 しかし、衝突の際に光子の数が保存されない場合がある。
アインシュタインの光電方程式:
プランクの量子論に基づいて、アインシュタインはアインシュタイン光電方程式として知られている光電効果の方程式を導きました。 アインシュタインは、
- 光は光子またはエネルギーの量子からなり、各光子のエネルギーはhνであると仮定しました。 hはプランク定数、νは光の周波数
- 入射した光子はそれぞれ原子内の電子に衝突し、そのエネルギーをすべて電子に与える。
- このエネルギーの一部は電子が金属の表面から出てくるために使われ、残りの部分は電子が放出する運動エネルギーとなります。
- 電子が金属の表面から出てくるために必要な最小のエネルギーを、金属の光電仕事関数(∅o)と呼びます。
- 残りのエネルギー(hν – ∅o)は、光電子が放出されるときの電子の最大運動エネルギーである。

この式はアインシュタインの光電方程式として知られている
光電仕事関数:
光電効果では、感光材料の原子の最も緩く付着した電子が除去される。 与えられた表面から電子を解放するのに必要な最小のエネルギーは、表面の材料の光電仕事関数(φo)と呼ばれる。 仕事関数は、金属表面の特徴的な特性である。
数学的に仕事関数は
∅o = h ννo
ここでν=閾値周波数、h=プランク定数で与えられます。
アインシュタインの光電方程式に基づく閾値周波数の存在の説明:
ある金属表面において、光電子は入射光の周波数が閾値周波数と呼ばれるある最小周波数以上のときのみ放出される。 閾値周波数はfordifferent物質、
アインシュタインの光電方程式によって

ここでνo=閾値周波数とh=プランク定数と
ν =入射光の周波数
運動エネルギーは常に非負の量ですすなわち、next。つまり、正またはゼロである。

このことは、光電効果のためには、入射放射線または入射光子の周波数が閾値周波数と同じかそれ以上でなければならないことを意味している。 原子によって確率的な光電子に作用する引力は異なる。
アインシュタインの光電方程式に基づく強度の効果の説明:
入射光の周波数が閾値周波数より小さい場合、入射光の強度がどんなに大きくても光電子は放出されません。
1秒間に放出される光電子の数は、入射光の強度に正比例します。 したがって、光電流は入射光の強度に正比例する。 光の強度が大きければ大きいほど、表面に入射する光子の数は多くなります。 光電子のtheincreased数が原因で光放出の速度が増加し、光電電流の強さが増加する。 したがって、光電効果(電流)は入射光の強さに正比例すると結論づけることができる。
アインシュタインの光電方程式に基づく最大運動エネルギーの可能性の説明。
アインシュタインの光電方程式

ここでνo=閾値周波数、h=プランク定数、
ν= 入射光の周波数
この方程式には強度の項はない。 したがって、光電子の最大運動エネルギーは、入射放射の強度に依存せず、入射放射の周波数に依存すると言える。 この式は、電子の最大運動エネルギーが入射放射の周波数に依存することを示している。
アインシュタインの光電方程式に基づく光電効果の瞬時性の説明:
光電効果は瞬時的なプロセスである。 光の入射と光電子の放出との間にタイムラグはなく、言い換えれば、光が当たると同時に表面から光電子が放出され始める。 また、光電子の放出は入射光が遮断された瞬間に停止します。
その瞬間、光放出面に放射線が入射すると、光子の全エネルギーが一挙に電子1個に伝達されます。 このように電子はタイムラグなく放出され、光電効果は瞬間的なプロセスです。
Previous Topic: 光電効果の数値問題
Next Topic: 光電方程式に関する数値問題
理科 > 物理学 > 光電効果 > アインシュタインの光電方程式
