Un grupo 
es un conjunto finito o infinito de elementos junto con una operación binaria (llamada operación de grupo) que juntos satisfacen las cuatro propiedades fundamentales de cierre, asociatividad, la propiedad de identidad y la propiedad inversa. La operación con respecto a la cual se define un grupo suele llamarse «operación de grupo», y se dice que un conjunto es un grupo «bajo» esta operación. Los elementos 
, 
, 
, … con operación binaria entre 
y 
denotada 
forman un grupo si
1. Cierre: Si 
y 
son dos elementos en 
, entonces el producto 
está también en 
.
2. Asociatividad: La multiplicación definida es asociativa, es decir, para todo 
, 
.
3. Identidad: Existe un elemento de identidad 
(también conocido como 1, 
, o 
) tal que 
para todo elemento 
.
4. Inverso: Debe haber un inverso (también llamado recíproco) de cada elemento. Por tanto, para cada elemento 
de 
, el conjunto contiene un elemento 
tal que 
.
Un grupo es un monoide cada uno de cuyos elementos es invertible.
Un grupo debe contener al menos un elemento, con el único (hasta el isomorfismo) grupo de un solo elemento conocido como el grupo trivial.
El estudio de los grupos se conoce como teoría de grupos. Si hay un número finito de elementos, el grupo se llama un grupo finito y el número de elementos se llama el orden del grupo. Un subconjunto de un grupo que es cerrado bajo la operación de grupo y la operación inversa se llama subgrupo. Los subgrupos también son grupos, y muchos grupos comúnmente encontrados son de hecho subgrupos especiales de algún grupo más general.
Un ejemplo básico de un grupo finito es el grupo simétrico 
, que es el grupo de permutaciones (o «bajo permutación») de 
objetos. El grupo infinito más sencillo es el conjunto de enteros bajo adición habitual. Para los grupos continuos, se pueden considerar los números reales o el conjunto de matrices invertibles 
. Estos dos últimos son ejemplos de grupos de Lie.
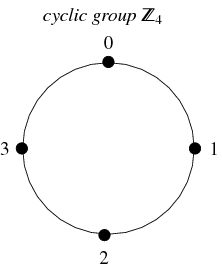
Un tipo de grupo muy común son los grupos cíclicos. Este grupo es isomorfo al grupo de los enteros (modulo 
), se denota 
, 
, o 
, y se define para cada entero 
. Es cerrado bajo adición, asociativo y tiene inversos únicos. Los números del 0 al 
representan sus elementos, con el elemento identidad representado por el 0, y el inverso de 
está representado por 
.
Un mapa entre dos grupos que preserva la identidad y la operación de grupo se llama homomorfismo. Si un homomorfismo tiene un inverso que también es un homomorfismo, entonces se llama isomorfismo y los dos grupos se llaman isomorfos. Dos grupos que son isomorfos entre sí se consideran «iguales» cuando se ven como grupos abstractos. Por ejemplo, el grupo de rotaciones de un cuadrado, ilustrado a continuación, es el grupo cíclico 
.
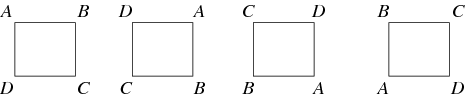
En general, una acción de grupo es cuando un grupo actúa sobre un conjunto, permutando sus elementos, de modo que el mapa del grupo al grupo de permutación del conjunto es un homomorfismo. Por ejemplo, las rotaciones de un cuadrado son un subgrupo de las permutaciones de sus vértices. Una acción de grupo importante para cualquier grupo 
es su acción sobre sí mismo por conjugación. Estos son sólo algunos de los posibles automorfismos de grupo. Otro tipo importante de acción de grupo es una representación de grupo, donde el grupo actúa sobre un espacio vectorial mediante mapas lineales invertibles. Cuando el campo del espacio vectorial son los números complejos, a veces una representación se llama módulo CG.
Las acciones de grupo, y en particular las representaciones, son muy importantes en las aplicaciones, no sólo a la teoría de grupos, sino también a la física y la química. Dado que se puede pensar en un grupo como un objeto matemático abstracto, el mismo grupo puede surgir en diferentes contextos. Por lo tanto, es útil pensar en una representación del grupo como una encarnación particular del grupo, que también puede tener otras representaciones. Una representación irreducible de un grupo es una representación para la que no existe ninguna transformación unitaria que transforme la matriz de representación en forma de diagonal de bloque. Las representaciones irreducibles tienen una serie de propiedades notables, como se formaliza en el teorema de ortogonalidad del grupo.