Le critère d’information bayésien (BIC) est un critère de sélection de modèles parmi un ensemble fini de modèles. Il est basé, en partie, sur la fonction de vraisemblance, et il est étroitement lié au critère d’information d’Akaike (AIC).
Lors de l’ajustement des modèles, il est possible d’augmenter la vraisemblance en ajoutant des paramètres, mais ce faisant, on peut aboutir à un surajustement. Le BIC résout ce problème en introduisant un terme de pénalité pour le nombre de paramètres dans le modèle. Le terme de pénalité est plus grand dans le BIC que dans l’AIC.
Le BIC a été largement utilisé pour l’identification de modèles dans les séries temporelles et la régression linéaire. Il peut cependant être appliqué assez largement à tout ensemble de modèles basés sur le maximum de vraisemblance.
Mathématiquement, le BIC peut être défini comme…
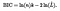

Application &Interprétation :
Les modèles peuvent être testés en utilisant les valeurs BIC correspondantes. Une valeur BIC inférieure indique des termes de pénalité plus faibles donc un meilleur modèle.
Lisez aussi les statistiques AIC.
Bien que ces deux mesures soient dérivées d’une perspective différente, elles sont étroitement liées. Apparemment, la seule différence est que le BIC considère le nombre d’observations dans la formule, ce que l’AIC ne fait pas.
Bien que le BIC soit toujours supérieur à l’AIC, plus la valeur de ces deux mesures est faible, meilleur est le modèle.
Données d’entraînement:
Visitez notre plateforme de science des données et d’analyse, Analyttica TreasureHunt pour vous entraîner sur de vrais ensembles de données.
Lisez également ce qui suit:
Vérification de la concordance.
Filtre à noyau.
Clustering k-Means.
