
Pythagore de Samos (vers 570-495… BCE)
Biographie – Qui était Pythagore
On prétend parfois que nous devons les mathématiques pures à Pythagore, et il est souvent appelé le premier « vrai » mathématicien. Mais, bien que sa contribution ait été clairement importante, il reste néanmoins une figure controversée.
Il n’a pas laissé d’écrits mathématiques lui-même, et la plupart de ce que nous savons de la pensée pythagoricienne nous vient des écrits de Philolaus et d’autres érudits pythagoriciens ultérieurs. En effet, il n’est pas du tout clair si beaucoup (ou même aucun) des théorèmes qui lui sont attribués ont en fait été résolus par Pythagore personnellement ou par ses disciples.
L’école qu’il a établie à Croton dans le sud de l’Italie vers 530 avant J.-C. était le noyau d’une secte pythagoricienne plutôt bizarre. Bien que la pensée pythagoricienne ait été largement dominée par les mathématiques, elle était également profondément mystique, et Pythagore a imposé ses philosophies quasi-religieuses, son végétarisme strict, sa vie en communauté, ses rites secrets et ses règles bizarres à tous les membres de son école (y compris des édits bizarres et apparemment aléatoires concernant le fait de ne jamais uriner en direction du soleil, de ne jamais épouser une femme qui porte des bijoux en or, de ne jamais croiser un âne couché dans la rue, de ne jamais manger ou même toucher des fèves noires, etc…) .
Les membres étaient divisés entre les « mathematikoi » (ou « apprenants »), qui prolongeaient et développaient les travaux plus mathématiques et scientifiques que Pythagore lui-même avait commencés, et les « akousmatikoi » (ou « auditeurs »), qui se concentraient sur les aspects plus religieux et rituels de ses enseignements. Il y a toujours eu un certain nombre de frictions entre les deux groupes et la secte a fini par être impliquée dans de violents combats locaux et s’est finalement dispersée. Le ressentiment s’est accumulé contre le secret et l’exclusivité des pythagoriciens et, en 460 avant Jésus-Christ, tous leurs lieux de réunion ont été brûlés et détruits, et au moins 50 membres ont été tués dans la seule ville de Croton.
Le dicton dominant de l’école de Pythagore était « Tout est nombre » ou « Dieu est nombre », et les pythagoriciens pratiquaient effectivement une sorte de numérologie ou de culte des nombres, et considéraient que chaque nombre avait son propre caractère et sa propre signification. Par exemple, le nombre un était le générateur de tous les nombres ; deux représentait l’opinion ; trois, l’harmonie ; quatre, la justice ; cinq, le mariage ; six, la création ; sept, les sept planètes ou « étoiles errantes » ; etc. Les nombres impairs étaient considérés comme féminins et les nombres pairs comme masculins.
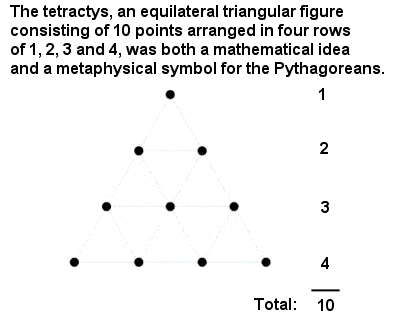
La Tetractys pythagoricienne
Le nombre le plus sacré de tous était la « Tetractys » ou dix, un nombre triangulaire composé de la somme de un, deux, trois et quatre. C’est un grand hommage aux réalisations intellectuelles des Pythagoriciens qu’ils aient déduit la place spéciale du nombre 10 à partir d’un argument mathématique abstrait plutôt qu’à partir de quelque chose d’aussi banal que de compter les doigts de deux mains.
Cependant, Pythagore et son école – ainsi qu’une poignée d’autres mathématiciens de la Grèce antique – a été largement responsable de l’introduction d’une mathématique plus rigoureuse que ce qui avait été fait auparavant, en construisant à partir des premiers principes en utilisant des axiomes et la logique. Avant Pythagore, par exemple, la géométrie n’avait été qu’un ensemble de règles dérivées de mesures empiriques.
Pythagore a découvert qu’il était possible de construire un système complet de mathématiques, où les éléments géométriques correspondaient à des nombres, et où les nombres entiers et leurs rapports étaient tout ce qui était nécessaire pour établir un système entier de logique et de vérité.
Le théorème de Pythagore
On se souvient principalement de lui pour ce qui est devenu le théorème de Pythagore (ou théorème de Pythagore) : que, pour tout triangle rectangle, le carré de la longueur de l’hypoténuse (le côté le plus long, opposé à l’angle droit) est égal à la somme du carré des deux autres côtés (ou « jambes »).
Ecrit sous forme d’équation : a2 + b2 = c2.
Ce que Pythagore et ses disciples n’ont pas réalisé, c’est que cela fonctionne également pour n’importe quelle forme : ainsi, l’aire d’un pentagone sur l’hypoténuse est égale à la somme des pentagones sur les deux autres côtés, comme pour un demi-cercle ou toute autre forme régulière (ou même irrégulière).
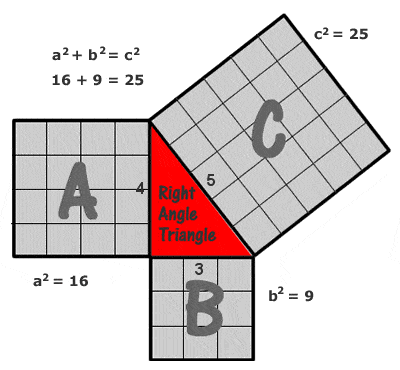
Théorème de Pythagore (Pythagore)
L’exemple le plus simple et le plus souvent cité d’un triangle pythagoricien est celui dont les côtés sont de 3, 4 et 5 unités (32 + 42 = 52, comme on peut le voir en dessinant une grille de carrés d’unités sur chaque côté comme dans le schéma de droite), mais il existe un nombre potentiellement infini d’autres « triangles de Pythagore » entiers, à commencer par (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), etc. Il faut cependant noter que (6, 8, 10) n’est pas ce que l’on appelle un triple pythagoricien « primitif », car il n’est qu’un multiple de (3, 4, 5).
Le théorème de Pythagore et les propriétés des triangles rectangles semblent être le développement mathématique le plus ancien et le plus répandu après l’arithmétique et la géométrie de base, et il a été abordé dans certains des plus anciens textes mathématiques de Babylone et d’Égypte, datant de plus de mille ans auparavant. L’une des preuves les plus simples provient de la Chine ancienne et date probablement de bien avant la naissance de Pythagore. C’est toutefois Pythagore qui a donné au théorème sa forme définitive, bien qu’il ne soit pas clair si Pythagore lui-même l’a définitivement prouvé ou s’il l’a simplement décrit. Quoi qu’il en soit, il est devenu l’un des théorèmes mathématiques les plus connus, et il existe aujourd’hui pas moins de 400 preuves différentes, certaines géométriques, d’autres algébriques, d’autres encore impliquant des équations différentielles avancées, etc.
Il est cependant devenu très vite évident que des solutions non entières étaient également possibles, de sorte qu’un triangle isocèle avec des côtés 1, 1 et √2, par exemple, a également un angle droit, comme les Babyloniens l’avaient découvert des siècles plus tôt. Cependant, lorsque Hippasus, l’élève de Pythagore, a essayé de calculer la valeur de √2, il a constaté qu’il n’était pas possible de l’exprimer sous forme de fraction, indiquant ainsi l’existence potentielle d’un tout nouveau monde de nombres, les nombres irrationnels (nombres qui ne peuvent pas être exprimés sous forme de simples fractions d’entiers). Cette découverte a plutôt brisé l’élégant monde mathématique construit par Pythagore et ses disciples, et l’existence d’un nombre qui ne pouvait pas être exprimé comme le rapport de deux créations de Dieu (ce qui est la façon dont ils pensaient aux nombres entiers) a mis en péril tout le système de croyance du culte.
Le pauvre Hippasus a apparemment été noyé par les pythagoriciens secrets pour avoir diffusé cette importante découverte au monde extérieur. Mais le remplacement de l’idée de la divinité des entiers par le concept plus riche du continuum, a été un développement essentiel des mathématiques. Il a marqué la véritable naissance de la géométrie grecque, qui traite des lignes et des plans et des angles, qui sont tous continus et non discrets.
Parmi ses autres réalisations en géométrie, Pythagore (ou du moins ses disciples, les pythagoriciens) a également réalisé que la somme des angles d’un triangle est égale à deux angles droits (180°), et probablement aussi la généralisation qui stipule que la somme des angles intérieurs d’un polygone à n côtés est égale à (2n – 4) angles droits, et que la somme de ses angles extérieurs est égale à 4 angles droits. Ils étaient capables de construire des figures d’une aire donnée, et d’utiliser une algèbre géométrique simple, par exemple pour résoudre des équations telles que a(a – x) = x2 par des moyens géométriques.
Les pythagoriciens ont également établi les bases de la théorie des nombres, avec leurs investigations sur les nombres triangulaires, carrés et aussi parfaits (nombres qui sont la somme de leurs diviseurs). Ils ont découvert plusieurs nouvelles propriétés des nombres carrés, comme le fait que le carré d’un nombre n est égal à la somme des n premiers nombres impairs (par exemple, 42 = 16 = 1 + 3 + 5 + 7). Ils ont également découvert au moins la première paire de nombres amicables, 220 et 284 (les nombres amicables sont des paires de nombres pour lesquelles la somme des diviseurs d’un nombre est égale à l’autre nombre, par exemple les diviseurs propres de 220 sont 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 et 110, dont la somme est 284 ; et les diviseurs propres de 284 sont 1, 2, 4, 71 et 142, dont la somme est 220).
Théorie musicale
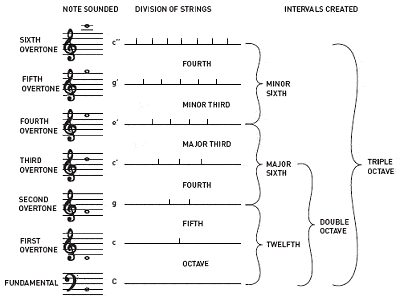
Pythagore est crédité de la découverte des rapports entre les tons musicaux harmonieux
Pythagore est également crédité de la découverte que les intervalles entre les notes musicales harmonieuses ont toujours des rapports en nombres entiers. Par exemple, jouer la moitié de la longueur d’une corde de guitare donne la même note que la corde à vide, mais une octave plus haut ; un tiers de la longueur donne une note différente mais harmonieuse ; etc.
Les rapports de nombres non entiers, en revanche, ont tendance à donner des sons dissonants. C’est ainsi que Pythagore a décrit les quatre premières harmoniques qui créent les intervalles communs qui sont devenus les principaux éléments constitutifs de l’harmonie musicale : l’octave (1:1), la quinte parfaite (3:2), la quarte parfaite (4:3) et la tierce majeure (5:4). La plus ancienne façon d’accorder la gamme chromatique de 12 notes est connue sous le nom d’accordage pythagoricien, et elle est basée sur un empilement de quintes parfaites, chacune accordée dans le rapport 3:2.
Le mystique Pythagore fut si excité par cette découverte qu’il devint convaincu que l’univers entier était basé sur des nombres, et que les planètes et les étoiles se déplaçaient selon des équations mathématiques, qui correspondaient à des notes de musique, et produisaient ainsi une sorte de symphonie, la « Musical Universalis » ou « Musique des sphères ».
| << Retour aux mathématiques grecques | En avant vers Platon >> |
.
