Nous savons comment trouver la racine carrée de tout nombre réel positif. De la même manière, nous pouvons trouver la racine carrée d’un nombre négatif. La différence est que la racine n’est pas réelle. Si la valeur du radicande est négative, on dit que la racine est un nombre imaginaire. Le nombre imaginaire i est défini comme la racine carrée de 1 négatif.
Donc, en utilisant les propriétés des radicaux,
Nous pouvons écrire la racine carrée de tout nombre négatif comme un multiple de i. Considérons la racine carrée de -25.
Nous utilisons 5i et non -\text{5}i\\\ parce que la racine principale de 25 est la racine positive.
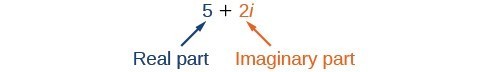
Figure 1
Un nombre complexe est la somme d’un nombre réel et d’un nombre imaginaire. Un nombre complexe est exprimé sous forme standard lorsqu’il est écrit a + bi où a est la partie réelle et bi est la partie imaginaire. Par exemple, 5+2i\\ est un nombre complexe. Il en est de même pour 3+4\sqrt{3}i\\\\.
Les nombres imaginaires se distinguent des nombres réels parce qu’un nombre imaginaire élevé au carré produit un nombre réel négatif. Rappelons que lorsqu’un nombre réel positif est élevé au carré, le résultat est un nombre réel positif et que lorsqu’un nombre réel négatif est élevé au carré, là encore, le résultat est un nombre réel positif. Les nombres complexes sont une combinaison de nombres réels et imaginaires.
Une note générale : nombres imaginaires et complexes
Un nombre complexe est un nombre de la forme a+bi\\\ où
- a est la partie réelle du nombre complexe.
- bi est la partie imaginaire du nombre complexe.
Si b=0\\\\, alors a+bi\\\ est un nombre réel. Si a=0\\\ et que b n’est pas égal à 0, le nombre complexe est appelé un nombre imaginaire. Un nombre imaginaire est une racine paire d’un nombre négatif.
Comment faire : étant donné un nombre imaginaire, l’exprimer sous forme standard.
- Ecrire \sqrt{-a}\\N comme \sqrt{a}\Nsqrt{-1}\N
- Exprimer \sqrt{-1}\N comme i.
- Ecrire \sqrt{a}\cdot i\N dans la forme la plus simple.
Exemple 1 : Exprimer un nombre imaginaire sous forme standard
Exprimer \sqrt{-9}\\ sous forme standard.
Solution
\sqrt{-9}=\sqrt{9}\sqrt{-1}=3i\\\
Sous forme standard, on obtient 0+3i\\\.
Essayez-le 1
Exprimez \sqrt{-24}\\\\ sous forme standard.
Solution
