Dans cette section, nous allons nous familiariser avec les opérations et les notations des ensembles, afin de pouvoir appliquer ces concepts à des problèmes de comptage et de probabilité. Nous commençons par définir certains termes.
Un ensemble est une collection d’objets, et ses membres sont appelés les éléments de l’ensemble. Nous nommons l’ensemble en utilisant des lettres majuscules, et nous entourons ses membres de crochets. Supposons que nous ayons besoin de lister les membres du club d’échecs. Nous utilisons la notation d’ensemble suivante.
C ={Ken, Bob, Tran, Shanti, Eric}
Un ensemble qui n’a pas de membres est appelé un ensemble vide. L’ensemble vide est désigné par le symbole Ø.
Deux ensembles sont égaux s’ils ont les mêmes éléments.
Un ensemble A est un sous-ensemble d’un ensemble B si chaque membre de A est aussi un membre de B.
Supposons que C = {Al, Bob, Chris, David, Ed} et A = {Bob, David}. Alors A est un sous-ensemble de C, écrit sous la forme 
.
Tout ensemble est un sous-ensemble de lui-même, et l’ensemble vide est un sous-ensemble de tout ensemble.
Union de deux ensembles
Disons que A et B sont deux ensembles, alors l’union de A et B, écrite sous la forme 
, est l’ensemble de tous les éléments qui sont soit dans A, soit dans B, soit à la fois dans A et dans B.
Intersection de deux ensembles
Si A et B sont deux ensembles, alors l’intersection de A et B, notée 
, est l’ensemble de tous les éléments qui sont communs aux deux ensembles A et B.
Un ensemble universel U est l’ensemble constitué de tous les éléments considérés.
Complément d’un ensemble
Que A soit un ensemble quelconque, alors le complément de l’ensemble A, écrit 
, est l’ensemble constitué des éléments de l’ensemble universel U qui ne sont pas dans A.
Ensembles disjoints
Deux ensembles A et B sont appelés ensembles disjoints si leur intersection est un ensemble vide.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {orange, vert, indigo, violet}Pour parvenir à une meilleure compréhension, supposons que l’ensemble universel U représente les couleurs du spectre, et P les couleurs primaires, alors représente les couleurs du spectre qui ne sont pas des couleurs primaires.
.
= {rouge, jaune, bleu, vert}
= {orange, indigo, violet}
= {rouge, jaune, bleu, violet} = {violet}Diagrammes de Venn
Nous utilisons maintenant les diagrammes de Venn pour illustrer les relations entre les ensembles. À la fin des années 1800, un logicien anglais nommé John Venn a développé une méthode pour représenter les relations entre les ensembles. Il a représenté ces relations à l’aide de diagrammes, qui sont maintenant connus sous le nom de diagrammes de Venn. Un diagramme de Venn représente un ensemble comme l’intérieur d’un cercle. Souvent, deux ou plusieurs cercles sont enfermés dans un rectangle où le rectangle représente l’ensemble universel. Il est facile de visualiser l’intersection ou l’union d’un ensemble. Dans cette section, nous utiliserons principalement les diagrammes de Venn pour trier diverses populations et compter des objets.
|
(a) |
(b) |
(c) |
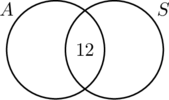
Parce que 30 personnes conduisent des voitures à transmission automatique, le cercle A doit contenir 30 éléments. Cela signifie que x + 12 = 30, ou x = 18. De même, puisque 20 personnes ont conduit des voitures à transmission standard, le cercle B doit contenir 20 éléments, soit y +12 = 20, ce qui fait que y = 8.
Maintenant que toutes les informations sont triées, il est facile de lire sur le diagramme que 18 personnes ont conduit des voitures à transmission automatique uniquement, 12 personnes ont conduit les deux types de voitures et 8 ont conduit des voitures à transmission standard uniquement. Par conséquent, 18 + 12 + 8 = 38 personnes ont participé à l’enquête.
|
(a) |
(b) |
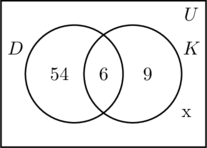
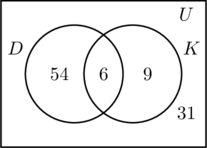
Nous remplissons les trois régions associées aux ensembles D et K de la même manière que précédemment. Puisque 100 personnes ont participé à l’enquête, le rectangle représentant l’ensemble universel U doit contenir 100 objets. Soit x qui représente les personnes de l’ensemble universel qui ne sont ni dans l’ensemble D ni dans K. Cela signifie que 54 + 6 + 9 + x = 100, soit x = 31.
Donc, il y a 31 personnes dans l’enquête qui n’ont visité aucun des deux endroits.
- 50 font du jogging, 30 de la natation et 35 du vélo
- 14 font du jogging et de la natation
- 7 font de la natation et du vélo
- 9 font du jogging et du vélo
- 3 personnes pratiquent les trois activités
Solution
|
(a) |
(b) |
(c) |
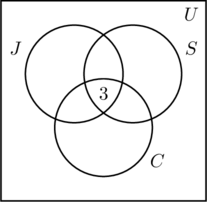
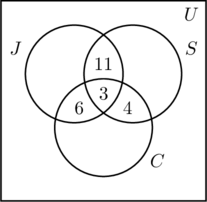
Nous plaçons un 3 dans la région la plus intérieure de la figure (a) car il représente le nombre de personnes qui participent aux trois activités. Ensuite, nous calculons x, y et z.
- Puisque 14 personnes font du jogging et nagent, x +3 = 14, ou x = 11.
- Le fait que 9 personnes font du jogging et du vélo donne y + 3 = 9, ou y = 6.
- Puisque 7 personnes font de la natation et du vélo, z + 3 = 7, ou z = 4.
- Cette information est représentée sur la figure (b).
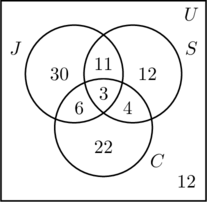
- Puisque 50 personnes font du jogging, m + 11 + 6 + 3 = 50, soit m = 30.
- 30 personnes nagent, donc n + 11 + 4 + 3 = 30, soit n = 12.
- 35 personnes font du vélo, donc p + 6 + 4 + 3 = 35, soit p = 22.
- En additionnant toutes les entrées des trois ensembles, on obtient une somme de 88. Puisque 100 personnes ont été sondées, le nombre à l’intérieur de l’ensemble universel mais à l’extérieur des trois ensembles est 100 – 88, soit 12.
- Dans la figure (c), l’information est triée, et on peut facilement répondre aux questions.
Questions pratiques
1. Soit l’ensemble universel U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h}, et W = {a, c, e, g, i}. Enumérez les membres des ensembles suivants :
a. 
b. 
2. Considérons les ensembles suivants : A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, Influenza, Norovirus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella}, et C = {SARS, Listeria, Tuberculose, H5N1, Salmonella, VIH, COVID-19}. Enumérez les membres des ensembles suivants :
a. 
b. 
3. Une enquête auprès des athlètes a révélé que pour leurs petits maux, 30 utilisaient de l’aspirine, 50 de l’ibuprofène et 15 les deux. Tous les athlètes interrogés ont utilisé au moins un des deux analgésiques. Combien d’athlètes ont été interrogés ?
4. Une étude portant sur 150 lycéens a révélé que 25 ont déclaré avoir déjà subi une commotion ou un traumatisme crânien, 52 ont déclaré avoir souffert d’une maladie mentale, et 15 ont déclaré les deux résultats. Combien d’étudiants n’ont déclaré aucun des deux résultats ?
5. Une enquête menée auprès de 100 étudiants de l’Université Ryerson révèle que 50 sont abonnés à Netflix, 40 sont abonnés à Amazon Prime et 30 sont abonnés à Disney+. Parmi ceux-ci, 15 sont abonnés à la fois à Netflix et à Amazon Prime, 10 à Amazon Prime et à Disney+, 10 à Netflix et à Disney+, et 5 ont les trois services d’abonnement. Dessinez un diagramme de Venn et déterminez les éléments suivants :
a. Le nombre d’étudiants abonnés à Amazon Prime mais pas aux deux autres services de streaming.
b. Le nombre d’étudiants abonnés à Netflix ou Amazon Prime mais pas à Disney+.
c. Le nombre d’étudiants ne s’abonnant à aucun de ces services.
c.