a.k.a. fiabilité inter-évaluateurs ou concordance
En statistique, la fiabilité inter-évaluateurs, l’accord inter-évaluateurs ou la concordance est le degré d’accord entre les évaluateurs. Il donne un score du degré d’homogénéité, ou de consensus, dans les notes données par les juges.
Les Kappa dont il est question ici sont les plus appropriés pour les données « nominales ». L’ordre naturel dans les données (s’il existe) est ignoré par ces méthodes. Si vous allez utiliser ces métriques assurez-vous d’être conscient des limites.
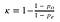
Il y a deux parties à cela :
- Calculer l’accord observé
- Calculer l’accord par hasard
Disons que nous avons affaire à des réponses « oui » et « non » et à 2 évaluateurs. Voici les évaluations:
rater1 =
rater2 =
Transformer ces évaluations en une matrice de confusion:

Observed agreement = (6 + 1) / 10 = 0.7
Chance agreement = probability of randomly saying yes (P_yes) + probability of randomly saying no (P_no)
P_yes = (6 + 1) / 10 * (6 + 1) / 10 = 0.49
P_no = (1 + 1) / 10 * (1 + 1) / 10 = 0.04
Chance agreement = 0.49 + 0.04 = 0.53
Puisque l’accord observé est plus grand que l’accord par hasard, nous aurons un Kappa positif.
kappa = 1 - (1 - 0.7) / (1 - 0.53) = 0.36
Ou simplement utiliser l’implémentation de sklearn
from sklearn.metrics import cohen_kappa_scorecohen_kappa_score(rater1, rater2)
qui renvoie 0,35714.
Interprétation de Kappa

Cas particuliers
Accord inférieur au hasard
rater1 =
rater2 =
cohen_kappa_score(rater1, rater2)
-0.2121
Si toutes les les évaluations sont identiques et opposées
Ce cas produit de manière fiable un kappa de 0
rater1 = * 10
rater2 = * 10
cohen_kappa_score(rater1, rater2)
0.0
Évaluations aléatoires
Pour les évaluations aléatoires, Kappa suit une distribution normale avec une moyenne d’environ zéro.
A mesure que le nombre de notations augmente, il y a moins de variabilité de la valeur de Kappa dans la distribution.
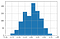
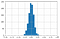
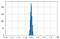
Vous trouverez plus de détails ici
Notez que le Kappa de Cohen ne s’applique qu’à 2 évaluateurs évaluant exactement les mêmes items.
