Un groupe 
est un ensemble fini ou infini d’éléments ainsi qu’une opération binaire (appelée opération de groupe) qui satisfont ensemble les quatre propriétés fondamentales de fermeture, d’associativité, la propriété d’identité et la propriété inverse. L’opération par rapport à laquelle un groupe est défini est souvent appelée » opération de groupe « , et on dit d’un ensemble qu’il est un groupe » sous » cette opération. Les éléments 
, 
, 
, … avec l’opération binaire entre 
et 
notée 
forment un groupe si
1. Fermeture : Si 
et 
sont deux éléments dans 
, alors le produit 
est aussi dans 
.
2. associativité : La multiplication définie est associative, c’est-à-dire que pour tout 
, 
.
3. identité : Il existe un élément d’identité 
(alias 1, 
, ou 
) tel que 
pour tout élément 
.
4. Inverse : Il doit y avoir un inverse (a.k.a. réciproque) de chaque élément. Par conséquent, pour chaque élément 
de 
, l’ensemble contient un élément 
tel que 
.
Un groupe est un monoïde dont chacun des éléments est inversible.
Un groupe doit contenir au moins un élément, le groupe unique (jusqu’à isomorphisme) à un seul élément étant appelé le groupe trivial.
L’étude des groupes est connue sous le nom de théorie des groupes. S’il y a un nombre fini d’éléments, le groupe est appelé un groupe fini et le nombre d’éléments est appelé l’ordre du groupe. Un sous-ensemble d’un groupe qui est fermé par l’opération de groupe et l’opération inverse s’appelle un sous-groupe. Les sous-groupes sont aussi des groupes, et de nombreux groupes couramment rencontrés sont en fait des sous-groupes spéciaux de quelque groupe plus général et plus grand.
Un exemple de base d’un groupe fini est le groupe symétrique 
, qui est le groupe des permutations (ou « sous permutation ») de 
objets. Le groupe infini le plus simple est l’ensemble des entiers sous addition usuelle. Pour les groupes continus, on peut considérer les nombres réels ou l’ensemble des matrices inversibles 
. Ces deux derniers sont des exemples de groupes de Lie.
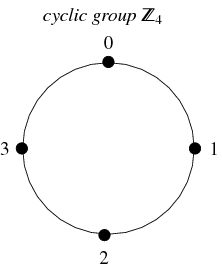
Un type de groupe très courant est celui des groupes cycliques. Ce groupe est isomorphe au groupe des entiers (modulo 
), est noté 
, 
, ou 
, et est défini pour tout entier 
. Il est fermé sous l’addition, associatif, et a des inverses uniques. Les nombres de 0 à 
représentent ses éléments, l’élément d’identité étant représenté par 0, et l’inverse de 
est représenté par 
.
Une carte entre deux groupes qui préserve l’identité et l’opération de groupe est appelée un homomorphisme. Si un homomorphisme a un inverse qui est aussi un homomorphisme, alors il est appelé un isomorphisme et les deux groupes sont appelés isomorphes. Deux groupes qui sont isomorphes l’un par rapport à l’autre sont considérés comme « identiques » lorsqu’ils sont considérés comme des groupes abstraits. Par exemple, le groupe des rotations d’un carré, illustré ci-dessous, est le groupe cyclique 
.
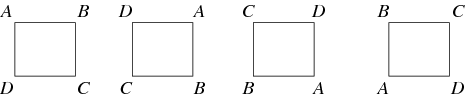
En général, une action de groupe est quand un groupe agit sur un ensemble, en permutant ses éléments, de sorte que la carte du groupe au groupe de permutation de l’ensemble est un homomorphisme. Par exemple, les rotations d’un carré sont un sous-groupe des permutations de ses coins. Une action de groupe importante pour tout groupe 
est son action sur lui-même par conjugaison. Ce ne sont là que quelques-uns des automorphismes de groupe possibles. Un autre type important d’action de groupe est une représentation de groupe, où le groupe agit sur un espace vectoriel par des cartes linéaires inversibles. Lorsque le champ de l’espace vectoriel est les nombres complexes, une représentation est parfois appelée un module CG.
Les actions de groupe, et en particulier les représentations, sont très importantes dans les applications, non seulement à la théorie des groupes, mais aussi à la physique et à la chimie. Comme un groupe peut être considéré comme un objet mathématique abstrait, le même groupe peut se présenter dans différents contextes. Il est donc utile de considérer une représentation du groupe comme une incarnation particulière du groupe, qui peut également avoir d’autres représentations. Une représentation irréductible d’un groupe est une représentation pour laquelle il n’existe pas de transformation unitaire qui transforme la matrice de représentation en forme de bloc diagonal. Les représentations irréductibles ont un certain nombre de propriétés remarquables, formalisées dans le théorème d’orthogonalité du groupe.