Le diagramme de phases de l’eau
La figure 11.23 « Deux versions du diagramme de phases de l’eau » montre le diagramme de phases de l’eau et illustre le fait que le point triple de l’eau se produit à 0,01°C et 0,00604 atm (4,59 mmHg). Bien plus reproductible que le point de fusion de la glace, qui dépend de la quantité d’air dissous et de la pression atmosphérique, le point triple (273,16 K) est utilisé pour définir l’échelle de température absolue (Kelvin). Le point triple représente également la pression la plus basse à laquelle une phase liquide peut exister en équilibre avec le solide ou la vapeur. Ainsi, à des pressions inférieures à 0,00604 atm, la glace ne fond pas en liquide lorsque la température augmente ; le solide se sublime directement en vapeur d’eau. La sublimation de l’eau à basse température et à basse pression peut être utilisée pour « lyophiliser » les aliments et les boissons. L’aliment ou la boisson est d’abord refroidi à des températures inférieures à zéro et placé dans un récipient dans lequel la pression est maintenue en dessous de 0,00604 atm. Puis, à mesure que la température augmente, l’eau se sublime, laissant l’aliment déshydraté (comme celui utilisé par les routards ou les astronautes) ou la boisson en poudre (comme pour le café lyophilisé).
Le diagramme de phase de l’eau illustré dans la partie (b) de la figure 11.23 » Deux versions du diagramme de phase de l’eau » montre la frontière entre la glace et l’eau sur une échelle élargie. La courbe de fusion de la glace est inclinée vers le haut et légèrement vers la gauche plutôt que vers le haut et la droite comme sur la figure 11.22 » Diagramme de phase typique d’une substance présentant trois phases – solide, liquide et gaz – et une région supercritique » ; c’est-à-dire que le point de fusion de la glace diminue avec l’augmentation de la pression ; à 100 MPa (987 atm), la glace fond à -9°C. L’eau se comporte ainsi parce qu’elle est l’une des rares substances connues pour lesquelles le solide cristallin est moins dense que le liquide (les autres sont l’antimoine et le bismuth). L’augmentation de la pression de la glace qui est en équilibre avec l’eau à 0°C et 1 atm tend à rapprocher certaines des molécules, diminuant ainsi le volume de l’échantillon. La diminution du volume (et l’augmentation correspondante de la densité) est plus faible pour un solide ou un liquide que pour un gaz, mais elle est suffisante pour faire fondre une partie de la glace.
Figure 11.23 Deux versions du diagramme de phase de l’eau
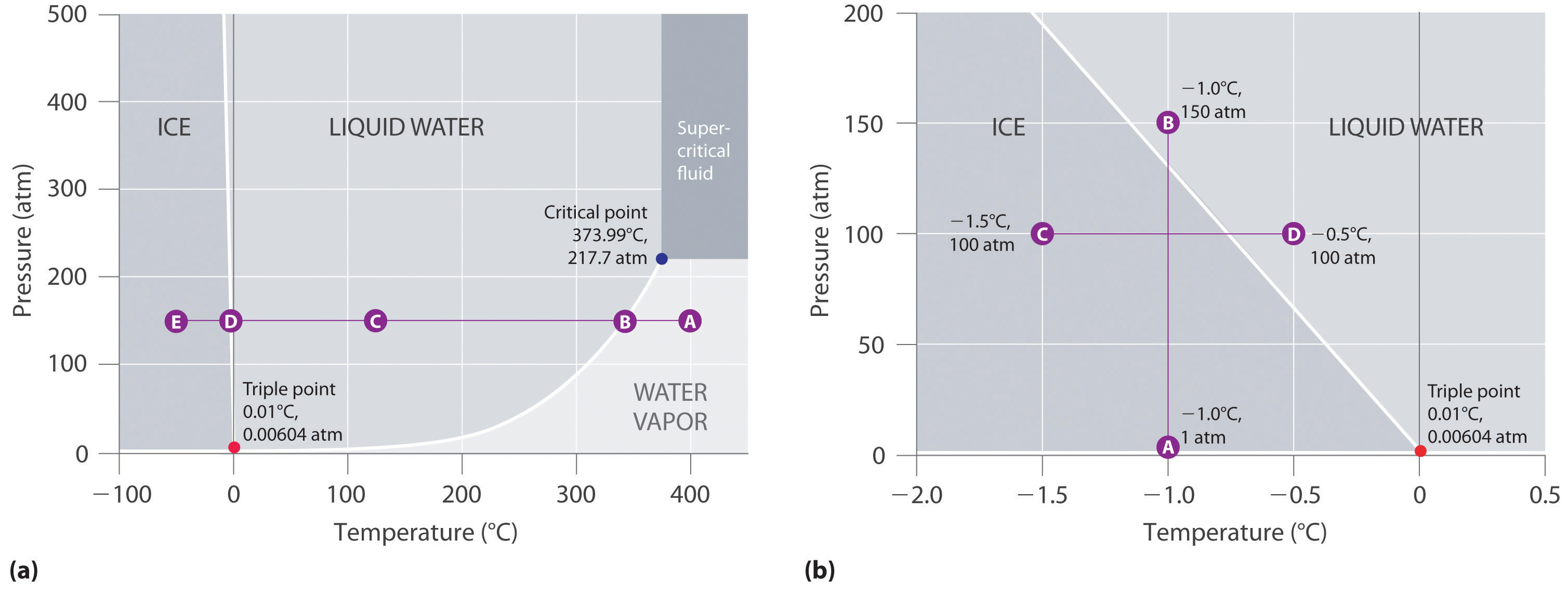
(a) Dans ce graphique avec des axes linéaires de température et de pression, la frontière entre la glace et l’eau liquide est presque verticale. (b) Ce graphique avec une échelle élargie illustre la diminution du point de fusion avec l’augmentation de la pression. (Les lettres font référence aux points discutés dans l’exemple 10.)
Dans la partie (b) de la figure 11.23 « Deux versions du diagramme de phase de l’eau », le point A est situé à P = 1 atm et T = -1,0°C, dans la région solide (glace) du diagramme de phase. Lorsque la pression augmente jusqu’à 150 atm alors que la température reste la même, la ligne du point A traverse la frontière glace/eau jusqu’au point B, qui se trouve dans la région de l’eau liquide. Par conséquent, l’application d’une pression de 150 atm fera fondre la glace à -1,0°C. Nous avons déjà indiqué que la dépendance du point de fusion de l’eau vis-à-vis de la pression est d’une importance capitale. Si la frontière solide/liquide dans le diagramme de phase de l’eau était inclinée vers le haut et vers la droite plutôt que vers la gauche, la glace serait plus dense que l’eau, les glaçons couleraient, les tuyaux d’eau n’éclateraient pas lorsqu’ils gèlent et l’antigel serait inutile dans les moteurs automobiles.
Jusqu’à récemment, de nombreux manuels décrivaient le patinage sur glace comme étant possible parce que la pression générée par la lame du patineur est suffisamment élevée pour faire fondre la glace sous la lame, créant ainsi une couche lubrifiante d’eau liquide qui permet à la lame de glisser sur la glace. Bien que cette explication soit intuitivement satisfaisante, elle est incorrecte, comme nous pouvons le montrer par un simple calcul. Rappelez-vous du chapitre 10 » Les gaz » que la pression (P) est la force (F) appliquée par unité de surface (A) :
Equation 11.4
P = F A
Pour calculer la pression qu’un patineur exerce sur la glace, nous devons calculer uniquement la force exercée et la surface de la lame du patin. Si nous supposons un patineur de 75,0 kg (165 lb), alors la force exercée par le patineur sur la glace en raison de la gravité est
Equation 11.5
F = mg
où m est la masse et g est l’accélération due à la gravité terrestre (9,81 m/s2). Ainsi, la force est
Equation 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Si nous supposons que les lames du patin ont 2.0 mm de large et 25 cm de long, alors la surface du fond de chaque lame est
Equation 11.7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Si le patineur glisse sur un pied, la pression exercée sur la glace est
Equation 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
Cette pression est beaucoup plus faible que celle nécessaire pour diminuer le point de fusion de la glace, même de 1°C, et l’expérience indique qu’il est possible de patiner même lorsque la température est bien inférieure au point de congélation. La fonte de la glace induite par la pression ne peut donc pas expliquer la faible friction qui permet aux patineurs (et aux palets de hockey) de glisser. Des recherches récentes indiquent que la surface de la glace, où le réseau ordonné de molécules d’eau rencontre l’air, est constituée d’une ou plusieurs couches d’eau presque liquide. Ces couches, ainsi que la fonte induite par la friction lorsque le patineur pousse vers l’avant, semblent expliquer à la fois la facilité avec laquelle un patineur glisse et le fait que le patinage devient plus difficile en dessous d’environ -7°C, lorsque le nombre de couches d’eau de surface lubrifiante diminue.
