Ciencia > Física >Efecto fotoeléctrico >Ecuación fotoeléctrica de Einstein
En este artículo, derivaremos la ecuación fotoeléctrica de Einstein y estudiaremos su uso para verificar las características del efecto fotoeléctrico de la luz.
Naturaleza ondulatoria de la luz:
Christian Huygen propuso que la luz se propaga en forma de onda. Pero esta teoría tiene un grave inconveniente. No fue capaz de explicar la propagación de la luz en el vacío. Este inconveniente fue eliminado por Maxwell, quien propuso que la luz es una onda electromagnética y que para la propagación de las ondas electromagnéticas no se requiere ningún medio material. Así se estableció la naturaleza ondulatoria de la luz.
La teoría ondulatoria fue capaz de explicar todos los fenómenos asociados a la propagación de la luz. Pero no pudo explicar la distribución de la energía y fenómenos modernos como el efecto fotoeléctrico, el efecto Crompton, etc.
Naturaleza de partícula de la luz:
Max Planck demostró que la propagación de la luz o de la energía tiene lugar en forma de paquetes de energía llamados cuantos. El quantum de luz se llama fotón y así estableció la naturaleza de partícula de la luz. Utilizando la naturaleza de partícula o cuántica de la radiación podemos explicar el fenómeno del efecto fotoeléctrico y el efecto Crompton.
Teoría Cuántica de Planck:
La teoría cuántica fue propuesta por Max Planck. Según esta teoría, la radiación de una fuente no se emite de forma continua, sino que se emite en paquetes o haces de energía. Estos paquetes se denominan cuantos o fotones. Si la radiación es de frecuencia ν, cada cuanto tiene una energía donde h es la constante de Planck.
Así, la energía del fotón = E = hν
La energía se emite de forma discontinua. Esto es contrario a la teoría clásica que asume que la emisión de energía es un proceso continuo.
Naturaleza de las partículas de las radiaciones electromagnéticas:
En la interacción de la radiación con la materia, la radiación se comporta como si estuviera formada por partículas. Estas partículas se llaman fotones. Cada fotón tiene una energía que viene dada por
E = hν = hc/λ
Todos los fotones de luz de una determinada frecuencia (longitud de onda) tienen la misma cantidad de energía asociada. El aumento de la intensidad de la luz aumenta el número de fotones por segundo a través de un área determinada, pero la energía de cada fotón será la misma. Los fotones son eléctricamente neutros y no se ven afectados por los campos eléctricos o magnéticos. Los fotones viajan en línea recta con la velocidad de la luz ‘c’, pero muestran difracción en ciertas condiciones.
El momento de cada fotón viene dado por
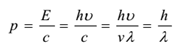
La longitud de onda del fotón cambia con el medio, por lo que tienen diferentesvelocidades en diferentes medios. La masa en reposo de un fotón es cero. Su masa cinética viene dada por
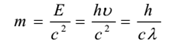
En una colisión entre partículas de fotones (como una colisión fotón-electrón) la energía y el momento totales se conservan. Sin embargo, el número de fotones puede no conservarse en una colisión. El fotón puede ser absorbido o se puede crear un nuevo fotón.
Ecuación fotoeléctrica de Einstein:
Sobre la base de la teoría cuántica de Planck, Einstein dedujo una ecuación para el efecto fotoeléctrico conocida como ecuación fotoeléctrica de Einstein. Einstein asumió que
- La luz consiste en fotones o cuantos de energía, la energía en cada fotón es hν. Donde h es la constante de Planck y ν es la frecuencia de la luz
- Cada fotón incidente colisiona con un electrón dentro de un átomo y cede toda su energía al electrón.
- Una parte de esta energía es utilizada por el electrón para salir de la superficie del metal y la parte restante es la energía cinética con la que se emite el electrón.
- La energía mínima que necesita un electrón para salir de la superficie del metal se denomina función de trabajo fotoeléctrico (∅o) del metal.
- La energía restante (hν – ∅o) es la energía cinética máxima del electrón con la que será expulsado un fotoelectrón.
Así, Energía cinética máxima del electrón = energía del fotón – función de trabajo
Sea ‘m’ la masa del electrón y vmax la velocidad máxima del fotoelectrón con la que será expulsado.

Esta ecuación se conoce como ecuación fotoeléctrica de Einstein
Función de trabajo fotoeléctrica:
En el efecto fotoeléctrico, se elimina el electrón más suelto de un átomo de material fotosensible. La energía mínima necesaria para liberar un electrón de la superficie dada se denomina función de trabajo fotoeléctrico (∅o) del material de la superficie. La función de trabajo es una propiedad característica de la superficie metálica.
Matemáticamente la función de trabajo viene dada por
∅o = h νo
Donde νo = frecuencia del umbral y h = constante de Planck.
Explicación de la existencia de la frecuencia umbral sobre la base de la ecuación fotoeléctrica de Einstein:
Para una superficie metálica determinada, los fotoelectrones se emiten sólo cuando la frecuencia de la luz incidente es mayor o igual a una determinada frecuencia mínima (no)conocida como frecuencia umbral. La frecuencia umbral es diferente para diferentes sustancias,
Por la ecuación fotoeléctrica de Einstein

Donde νo = frecuencia umbraly h = constante de Planck y
ν = frecuencia de la radiación incidente
La energía cinética es siempre una cantidad no negativa, es decir.Es decir, puede ser positiva o nula así

Lo que indica que para el efecto fotoeléctrico, la frecuencia de la radiación incidente o del fotón incidente debe ser igual o mayor que la frecuencia umbral. La fuerza de atracción que actúa sobre probables fotoelectrones en diferentes átomos es diferente. Por lo tanto, la frecuencia umbral es diferente para las distintas sustancias.
Explicación del efecto de la intensidad sobre la base de la ecuación fotoeléctrica de Einstein:
Si la frecuencia de la luz incidente es menor que la frecuencia umbral, los fotoelectrones no se emiten, por muy grande que sea la intensidad de la luz incidente.
El número de fotoelectrones emitidos por segundo es directamente proporcional a la intensidad de la luz incidente. Por lo tanto, la corriente fotoeléctrica es directamente proporcional a la intensidad de la luz incidente. Si la intensidad de la luz es mayor, el número de fotones incidentes en la superficie es mayor. Debido al aumento del número de fotoelectrones, la tasa de fotoemisión aumenta, por lo que la fuerza de la corriente fotoeléctrica aumenta. Así podemos concluir que el efecto fotoeléctrico (corriente) es directamente proporcional a la intensidad de la radiación incidente.
Explicación de la posible energía cinética máxima sobre la base de la ecuación fotoeléctrica de Einstein:
Por la ecuación fotoeléctrica de Einstein

Donde νo = frecuencia de umbraly h = constante de Planck y
ν = frecuencia de la radiación incidente
La ecuación no contiene el término de intensidad, por lo que podemos decir que la energía cinética máxima del fotoelectrón es independiente de la intensidad de la radiación incidente, pero depende de la frecuencia de la radiación incidente. Esta ecuación indica que la energía cinética máxima del electrón depende de la frecuencia de la radiación incidente. Y si la frecuencia de la radiación incidente aumenta, la energía cinética del fotoelectrón también aumenta.
Explicación de la instantaneidad del efecto fotoeléctrico sobre la base de la ecuación fotoeléctrica de Einstein:
El efecto fotoeléctrico es un proceso instantáneo. No existe ningún lapso de tiempo entre la incidencia de la luz y la emisión de los fotoelectrones, en otras palabras, la superficie comienza a emitir fotoelectrones tan pronto como la luz incide sobre ella. Asimismo, la emisión de fotoelectrones se detiene en el momento en que se interrumpe la luz incidente.
Cuando la radiación incide sobre la superficie fotoemisora en ese instante, toda la energía del fotón se transfiere a un solo electrón de una sola vez. Así, el electrón se emite sin ningún desfase temporal y el efecto fotoeléctrico es el proceso instantáneo.
Tema anterior: Problemas numéricos sobre el efecto fotoeléctrico
Siguiente Tema: Problemas numéricos sobre la ecuación fotoeléctrica
