El diagrama de fase del agua
La figura 11.23 «Dos versiones del diagrama de fase del agua» muestra el diagrama de fase del agua e ilustra que el punto triple del agua se produce a 0,01°C y 0,00604 atm (4,59 mmHg). Mucho más reproducible que el punto de fusión del hielo, que depende de la cantidad de aire disuelto y de la presión atmosférica, el punto triple (273,16 K) se utiliza para definir la escala de temperatura absoluta (Kelvin). El punto triple también representa la presión más baja a la que puede existir una fase líquida en equilibrio con el sólido o el vapor. Por tanto, a presiones inferiores a 0,00604 atm, el hielo no se funde en líquido al aumentar la temperatura; el sólido se sublima directamente en vapor de agua. La sublimación del agua a baja temperatura y presión puede utilizarse para «liofilizar» alimentos y bebidas. El alimento o la bebida se enfría primero a temperaturas bajo cero y se coloca en un recipiente en el que la presión se mantiene por debajo de 0,00604 atm. A continuación, al aumentar la temperatura, el agua se sublima, dejando el alimento deshidratado (como el que utilizan los mochileros o los astronautas) o la bebida en polvo (como en el caso del café liofilizado).
El diagrama de fases del agua ilustrado en la parte (b) de la figura 11.23 «Dos versiones del diagrama de fases del agua» muestra el límite entre el hielo y el agua en una escala ampliada. La curva de fusión del hielo se inclina hacia arriba y ligeramente hacia la izquierda en lugar de hacia arriba y hacia la derecha como en la figura 11.22 «Diagrama de fase típico para una sustancia que presenta tres fases -sólida, líquida y gaseosa- y una región supercrítica»; es decir, el punto de fusión del hielo disminuye con el aumento de la presión; a 100 MPa (987 atm), el hielo se funde a -9°C. El agua se comporta así porque es una de las pocas sustancias conocidas en las que el sólido cristalino es menos denso que el líquido (otras son el antimonio y el bismuto). El aumento de la presión del hielo que está en equilibrio con el agua a 0°C y 1 atm tiende a empujar algunas de las moléculas para que se acerquen, disminuyendo así el volumen de la muestra. La disminución del volumen (y el correspondiente aumento de la densidad) es menor para un sólido o un líquido que para un gas, pero es suficiente para fundir parte del hielo.
Figura 11.23 Dos versiones del diagrama de fases del agua
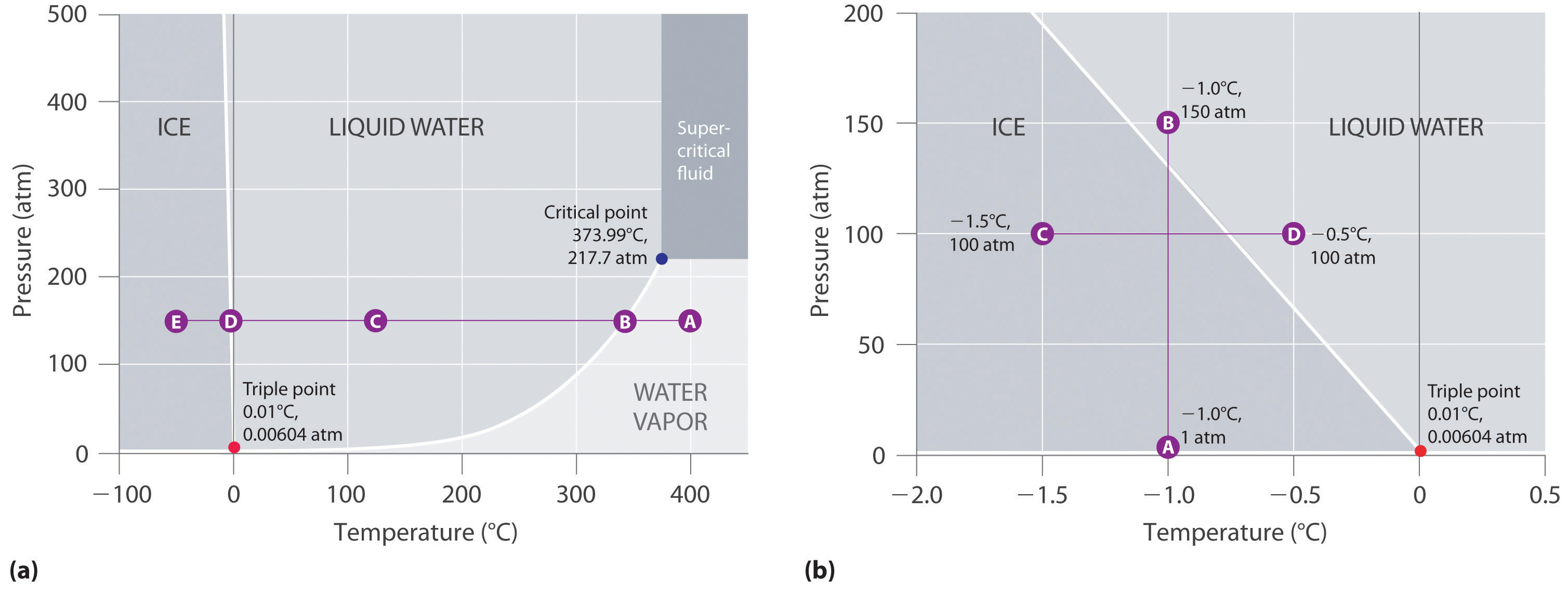
(a) En esta gráfica con ejes lineales de temperatura y presión, el límite entre el hielo y el agua líquida es casi vertical. (b) Este gráfico con una escala ampliada ilustra la disminución del punto de fusión con el aumento de la presión. (Las letras se refieren a los puntos discutidos en el ejemplo 10.)
En la parte (b) de la figura 11.23 «Dos versiones del diagrama de fases del agua», el punto A se encuentra a P = 1 atm y T = -1,0°C, dentro de la región sólida (hielo) del diagrama de fases. Al aumentar la presión a 150 atm mientras la temperatura permanece igual, la línea del punto A cruza el límite hielo/agua hasta el punto B, que se encuentra en la región del agua líquida. En consecuencia, si se aplica una presión de 150 atm se fundirá el hielo a -1,0°C. Ya hemos indicado que la dependencia de la presión del punto de fusión del agua es de vital importancia. Si el límite sólido/líquido en el diagrama de fases del agua se inclinara hacia arriba y hacia la derecha en lugar de hacia la izquierda, el hielo sería más denso que el agua, los cubitos de hielo se hundirían, las tuberías de agua no reventarían al congelarse y el anticongelante sería innecesario en los motores de los automóviles.
Hasta hace poco, muchos libros de texto describían que el patinaje sobre hielo era posible porque la presión generada por la cuchilla del patinador es lo suficientemente alta como para derretir el hielo bajo la cuchilla, creando así una capa lubricante de agua líquida que permite a la cuchilla deslizarse por el hielo. Aunque esta explicación es intuitivamente satisfactoria, es incorrecta, como podemos demostrar con un simple cálculo. Recordemos del capítulo 10 «Gases» que la presión (P) es la fuerza (F) aplicada por unidad de superficie (A):
Ecuación 11.4
P = F A
Para calcular la presión que ejerce un patinador sobre el hielo, necesitamos calcular sólo la fuerza ejercida y el área de la cuchilla del patín. Si suponemos un patinador de 75,0 kg (165 lb), entonces la fuerza que ejerce el patinador sobre el hielo debido a la gravedad es
Ecuación 11.5
F = mg
donde m es la masa y g es la aceleración debida a la gravedad terrestre (9,81 m/s2). Por tanto, la fuerza es
Ecuación 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Si suponemos que las cuchillas del patín tienen 2.0 mm de ancho y 25 cm de largo, entonces el área de la parte inferior de cada pala es
Ecuación 11.7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Si el patinador se desliza sobre un pie, la presión ejercida sobre el hielo es
Ecuación 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
La presión es mucho menor que la necesaria para disminuir el punto de fusión del hielo incluso en 1°C, y la experiencia indica que es posible patinar incluso cuando la temperatura está muy por debajo del punto de congelación. Por tanto, la fusión del hielo inducida por la presión no puede explicar la baja fricción que permite a los patinadores (y a los discos de hockey) deslizarse. Investigaciones recientes indican que la superficie del hielo, donde el conjunto ordenado de moléculas de agua se encuentra con el aire, está formada por una o más capas de agua casi líquida. Estas capas, junto con el derretimiento inducido por la fricción a medida que el patinador avanza, parecen explicar tanto la facilidad con la que un patinador se desliza como el hecho de que el patinaje se vuelve más difícil por debajo de unos -7°C, cuando el número de capas de agua superficial lubricante disminuye.
