Das Bayessche Informationskriterium (BIC) ist ein Kriterium für die Modellauswahl aus einer endlichen Menge von Modellen. Es basiert zum Teil auf der Likelihood-Funktion und ist eng mit dem Akaike-Informationskriterium (AIC) verwandt.
Bei der Anpassung von Modellen ist es möglich, die Likelihood durch Hinzufügen von Parametern zu erhöhen, was jedoch zu einer Überanpassung führen kann. Der BIC löst dieses Problem, indem er einen Strafterm für die Anzahl der Parameter im Modell einführt. Der Strafterm ist beim BIC größer als beim AIC.
Der BIC wird häufig zur Modellidentifikation bei Zeitreihen und linearen Regressionen verwendet. Es kann jedoch auf jeden Satz von Modellen auf der Grundlage der maximalen Wahrscheinlichkeit angewendet werden.
Mathematisch kann BIC definiert werden als.
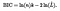

Anwendung & Interpretation:
Die Modelle können anhand der entsprechenden BIC-Werte getestet werden. Ein niedrigerer BIC-Wert deutet auf geringere Strafbedingungen und damit auf ein besseres Modell hin.
Lesen Sie auch die AIC-Statistik.
Obwohl diese beiden Maße aus einer anderen Perspektive abgeleitet werden, sind sie eng miteinander verwandt. Der einzige Unterschied besteht offenbar darin, dass BIC die Anzahl der Beobachtungen in der Formel berücksichtigt, was bei AIC nicht der Fall ist.
Obwohl BIC immer höher ist als AIC, ist der Wert dieser beiden Maße niedriger, je besser das Modell.
Praxisdatensatz:
Besuchen Sie unsere Data Science- und Analyseplattform, Analyttica TreasureHunt, um mit echten Datensätzen zu üben.
Lesen Sie auch Folgendes:
Übereinstimmungsprüfung.
Kernel-Filter.
k-Means Clustering.
