
Pythagoras von Samos (ca.570-495 BCE)
Biographie – Wer war Pythagoras
Es wird manchmal behauptet, dass wir die reine Mathematik Pythagoras verdanken, und er wird oft als der erste „echte“ Mathematiker bezeichnet. Doch obwohl sein Beitrag eindeutig wichtig war, bleibt er eine umstrittene Figur.
Er selbst hinterließ keine mathematischen Schriften, und vieles, was wir über das pythagoreische Denken wissen, stammt aus den Schriften von Philolaus und anderen späteren pythagoreischen Gelehrten. In der Tat ist keineswegs klar, ob viele (oder gar alle) der ihm zugeschriebenen Theoreme tatsächlich von Pythagoras persönlich oder von seinen Anhängern gelöst wurden.
Die von ihm um 530 v. Chr. in Croton in Süditalien gegründete Schule war die Keimzelle einer ziemlich bizarren pythagoreischen Sekte. Obwohl das pythagoreische Denken weitgehend von der Mathematik beherrscht wurde, war es auch zutiefst mystisch, und Pythagoras zwang allen Mitgliedern seiner Schule seine quasi-religiösen Philosophien, den strengen Vegetarismus, das Gemeinschaftsleben, geheime Riten und seltsame Regeln auf (einschließlich der bizarren und scheinbar willkürlichen Erlasse, niemals gegen die Sonne zu urinieren, niemals eine Frau zu heiraten, die Goldschmuck trägt, niemals an einem auf der Straße liegenden Esel vorbeizugehen, niemals schwarze Favabohnen zu essen oder auch nur zu berühren usw.) .
Die Mitglieder teilten sich in die „mathematikoi“ (oder „Lernenden“), die die eher mathematischen und wissenschaftlichen Arbeiten, die Pythagoras selbst begonnen hatte, erweiterten und weiterentwickelten, und die „akousmatikoi“ (oder „Zuhörer“), die sich auf die eher religiösen und rituellen Aspekte seiner Lehren konzentrierten. Zwischen den beiden Gruppen kam es immer wieder zu Reibereien, und schließlich wurde die Sekte in heftige lokale Kämpfe verwickelt und löste sich schließlich auf. Der Unmut über die Geheimniskrämerei und Exklusivität der Pythagoräer wuchs, und im Jahr 460 v. Chr. wurden alle ihre Versammlungsorte niedergebrannt und zerstört, wobei allein in Croton mindestens 50 Mitglieder getötet wurden.
Das übergeordnete Diktum der Schule des Pythagoras lautete: „Alles ist Zahl“ oder „Gott ist Zahl“, und die Pythagoräer praktizierten tatsächlich eine Art Numerologie oder Zahlenverehrung und waren der Ansicht, dass jede Zahl einen eigenen Charakter und eine eigene Bedeutung hatte. So war beispielsweise die Zahl Eins der Generator aller Zahlen, die Zwei stand für die Meinung, die Drei für die Harmonie, die Vier für die Gerechtigkeit, die Fünf für die Ehe, die Sechs für die Schöpfung, die Sieben für die sieben Planeten oder „Wandersterne“ usw. Ungerade Zahlen galten als weiblich und gerade Zahlen als männlich.
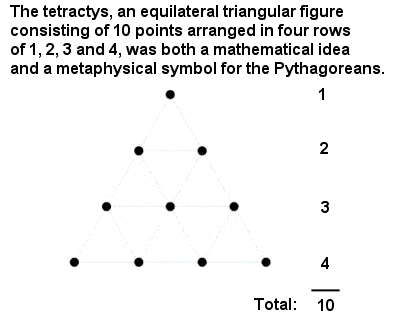
Die pythagoreische Tetraktys
Die heiligste Zahl von allen war „Tetraktys“ oder zehn, eine dreieckige Zahl, die sich aus der Summe von eins, zwei, drei und vier zusammensetzt. Es ist eine große Anerkennung für die intellektuellen Leistungen der Pythagoräer, dass sie die besondere Stellung der Zahl 10 aus einem abstrakten mathematischen Argument ableiteten und nicht aus etwas so Banalem wie dem Abzählen der Finger an zwei Händen.
Pythagoras und seine Schule – sowie eine Handvoll anderer Mathematiker des antiken Griechenlands – waren jedoch weitgehend für die Einführung einer strengeren Mathematik als die vorherige verantwortlich, die auf ersten Prinzipien unter Verwendung von Axiomen und Logik aufbaute. Vor Pythagoras zum Beispiel war die Geometrie lediglich eine Sammlung von Regeln, die durch empirische Messungen abgeleitet wurden.
Pythagoras entdeckte, dass ein vollständiges System der Mathematik konstruiert werden konnte, in dem geometrische Elemente mit Zahlen korrespondierten und in dem ganze Zahlen und ihre Verhältnisse alles waren, was notwendig war, um ein ganzes System von Logik und Wahrheit zu etablieren.
Der Satz des Pythagoras
Er ist vor allem für den Satz des Pythagoras (oder den Satz des Pythagoras) bekannt geworden: dass für jedes rechtwinklige Dreieck das Quadrat der Länge der Hypotenuse (der längsten Seite, die dem rechten Winkel gegenüberliegt) gleich der Summe der Quadrate der beiden anderen Seiten (oder „Schenkel“) ist.
Geschrieben als Gleichung: a2 + b2 = c2.
Was Pythagoras und seine Anhänger nicht wussten, ist, dass dies auch für jede beliebige Form gilt: So ist der Flächeninhalt eines Fünfecks auf der Hypotenuse gleich der Summe der Fünfecke auf den beiden anderen Seiten, wie es auch für einen Halbkreis oder jede andere regelmäßige (oder auch unregelmäßige) Form gilt.
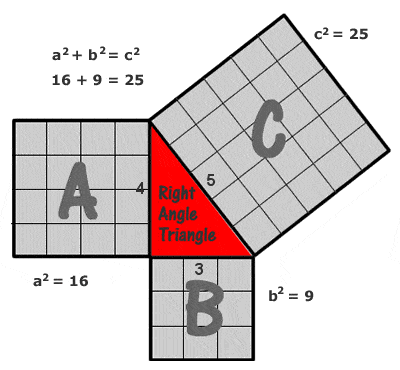
Satz des Pythagoras
Das einfachste und am häufigsten zitierte Beispiel eines pythagoräischen Dreiecks ist ein Dreieck mit den Seitenlängen 3, 4 und 5 Einheiten (32 + 42 = 52, wie man sieht, wenn man ein Gitter aus Einheitsquadraten auf jeder Seite zeichnet, wie im Diagramm rechts), aber es gibt eine potenziell unendliche Anzahl anderer ganzzahliger „pythagoräischer Dreiecke“, angefangen mit (5, 12, 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41) usw. Es sei jedoch darauf hingewiesen, dass (6, 8, 10) kein so genanntes „primitives“ pythagoräisches Tripel ist, da es nur ein Vielfaches von (3, 4, 5) ist.
Der Satz des Pythagoras und die Eigenschaften rechtwinkliger Dreiecke scheinen die älteste und am weitesten verbreitete mathematische Entwicklung nach den Grundrechenarten und der Geometrie zu sein, und sie wurden in einigen der ältesten mathematischen Texte aus Babylon und Ägypten behandelt, die mehr als tausend Jahre früher entstanden. Einer der einfachsten Beweise stammt aus dem alten China und stammt wahrscheinlich aus der Zeit vor Pythagoras‘ Geburt. Es war jedoch Pythagoras, der dem Satz seine endgültige Form gab, obwohl nicht klar ist, ob Pythagoras selbst ihn endgültig bewiesen oder nur beschrieben hat. Auf jeden Fall ist er zu einem der bekanntesten mathematischen Sätze geworden, und es gibt inzwischen bis zu 400 verschiedene Beweise, einige geometrisch, einige algebraisch, einige mit fortgeschrittenen Differentialgleichungen usw.
Es stellte sich jedoch bald heraus, dass auch nicht-ganzzahlige Lösungen möglich waren, so dass z. B. ein gleichschenkliges Dreieck mit den Seiten 1, 1 und √2 auch einen rechten Winkel hat, wie die Babylonier Jahrhunderte zuvor entdeckt hatten. Als jedoch der Schüler des Pythagoras, Hippasus, versuchte, den Wert von √2 zu berechnen, stellte er fest, dass es nicht möglich war, ihn als Bruch auszudrücken, was auf die mögliche Existenz einer ganz neuen Welt von Zahlen hinwies, den irrationalen Zahlen (Zahlen, die nicht als einfache Brüche ganzer Zahlen ausgedrückt werden können). Diese Entdeckung brachte die elegante mathematische Welt, die Pythagoras und seine Anhänger aufgebaut hatten, ziemlich ins Wanken, und die Existenz einer Zahl, die sich nicht als Verhältnis zweier göttlicher Schöpfungen ausdrücken ließ (wie sie sich die ganzen Zahlen vorstellten), gefährdete das gesamte Glaubenssystem des Kults.
Der arme Hippasus wurde offenbar von den geheimnisvollen Pythagoräern ertränkt, weil er diese wichtige Entdeckung nach außen getragen hatte. Aber die Ersetzung der Idee der Göttlichkeit der ganzen Zahlen durch das umfassendere Konzept des Kontinuums war eine wesentliche Entwicklung in der Mathematik. Sie war die eigentliche Geburtsstunde der griechischen Geometrie, die sich mit Linien, Ebenen und Winkeln beschäftigt, die alle kontinuierlich und nicht diskret sind.
Neben seinen anderen Errungenschaften in der Geometrie erkannte Pythagoras (oder zumindest seine Anhänger, die Pythagoräer) auch, dass die Summe der Winkel eines Dreiecks gleich zwei rechten Winkeln (180°) ist, und wahrscheinlich auch die Verallgemeinerung, die besagt, dass die Summe der Innenwinkel eines Polygons mit n Seiten gleich (2n – 4) rechten Winkeln ist, und dass die Summe der Außenwinkel gleich 4 rechten Winkeln ist. Sie waren in der Lage, Figuren mit einem bestimmten Flächeninhalt zu konstruieren und einfache geometrische Algebra zu verwenden, um zum Beispiel Gleichungen wie a(a – x) = x2 mit geometrischen Mitteln zu lösen.
Die Pythagoräer legten auch die Grundlagen der Zahlentheorie mit ihren Untersuchungen von Dreiecks-, Quadratzahlen und auch vollkommenen Zahlen (Zahlen, die die Summe ihrer Teiler sind). Sie entdeckten mehrere neue Eigenschaften von Quadratzahlen, wie zum Beispiel, dass das Quadrat einer Zahl n gleich der Summe der ersten n ungeraden Zahlen ist (z. B. 42 = 16 = 1 + 3 + 5 + 7). Sie entdeckten auch mindestens das erste Paar gütiger Zahlen, 220 und 284 (gütige Zahlen sind Zahlenpaare, bei denen die Summe der Teiler der einen Zahl gleich der anderen Zahl ist, z. B. sind die richtigen Teiler von 220 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 und 110, deren Summe 284 ist; und die richtigen Teiler von 284 sind 1, 2, 4, 71 und 142, deren Summe 220 ist).
Musiktheorie
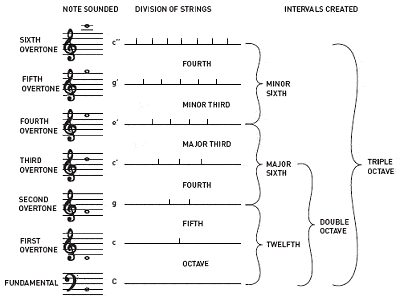
Pythagoras wird die Entdeckung der Verhältnisse zwischen harmonischen Musiktönen zugeschrieben
Pythagoras wird auch die Entdeckung zugeschrieben, dass die Intervalle zwischen harmonischen Musiktönen immer ganzzahlige Verhältnisse haben. Wenn man z.B. eine halbe Gitarrensaite spielt, erhält man den gleichen Ton wie die leere Saite, aber eine Oktave höher; ein Drittel einer Saite ergibt einen anderen, aber harmonischen Ton usw.
Nicht-ganzzahlige Verhältnisse führen dagegen eher zu dissonanten Tönen. Auf diese Weise beschrieb Pythagoras die ersten vier Obertöne, die die gemeinsamen Intervalle bilden, die zu den Grundbausteinen der musikalischen Harmonie geworden sind: die Oktave (1:1), die reine Quinte (3:2), die reine Quarte (4:3) und die große Terz (5:4). Die älteste Art, die 12-stimmige chromatische Tonleiter zu stimmen, ist als pythagoreische Stimmung bekannt und basiert auf einem Stapel perfekter Quinten, die jeweils im Verhältnis 3:2 gestimmt sind.
Der mystische Pythagoras war von dieser Entdeckung so begeistert, dass er zu der Überzeugung gelangte, dass das gesamte Universum auf Zahlen basiert und dass sich die Planeten und Sterne nach mathematischen Gleichungen bewegen, die den musikalischen Noten entsprechen, und so eine Art Symphonie, die „Musical Universalis“ oder „Musik der Sphären“, hervorbringen.
| << Zurück zur griechischen Mathematik | Vorwärts zu Platon >> |
