- Lernziele
- Beispiel 1. Berechnung der Photonenenergie und des photoelektrischen Effekts: Ein violettes Licht
- Strategie
- Lösung für Teil 1
- Lösung für Teil 2
- Diskussion
- PhET Explorations: Photoelektrischer Effekt
- Zusammenfassung des Abschnitts
- Konzeptuelle Fragen
- Probleme & Übungen
- Glossar
- Ausgewählte Lösungen zu Aufgaben & Übungen
Lernziele
Am Ende dieses Abschnitts können Sie:
- Beschreiben Sie ein typisches Experiment zum photoelektrischen Effekt.
- Bestimmen Sie die maximale kinetische Energie von Photoelektronen, die von Photonen einer Energie oder Wellenlänge ausgestoßen werden, wenn Sie die maximale kinetische Energie von Photoelektronen für eine andere Photonenenergie oder Wellenlänge erhalten.
Wenn Licht auf Materialien trifft, kann es Elektronen aus ihnen herausschlagen. Dies wird als photoelektrischer Effekt bezeichnet, was bedeutet, dass Licht (Photo) Elektrizität erzeugt. Eine häufige Anwendung des photoelektrischen Effekts sind Belichtungsmesser, z. B. solche, die die automatische Blende bei verschiedenen Kameratypen einstellen. In ähnlicher Weise wird der photoelektrische Effekt auch in Solarzellen verwendet, wie Sie sie wahrscheinlich in Ihrem Taschenrechner haben oder auf einem Dach oder einem Straßenschild gesehen haben. Diese nutzen den photoelektrischen Effekt, um Licht in Elektrizität für den Betrieb verschiedener Geräte umzuwandeln.

Abbildung 1. Der photoelektrische Effekt kann beobachtet werden, indem man Licht auf die Metallplatte in dieser evakuierten Röhre fallen lässt. Die vom Licht ausgestoßenen Elektronen werden auf dem Kollektordraht gesammelt und als Strom gemessen. Eine Verzögerungsspannung zwischen dem Kollektordraht und der Platte kann dann so eingestellt werden, dass die Energie der ausgestoßenen Elektronen bestimmt wird. Ist die Spannung zum Beispiel ausreichend negativ, erreichen keine Elektronen den Draht. (credit: P.P. Urone)
Dieser Effekt ist seit mehr als einem Jahrhundert bekannt und kann mit einer Vorrichtung wie der in Abbildung 1 dargestellten untersucht werden. Diese Abbildung zeigt eine evakuierte Röhre mit einer Metallplatte und einem Kollektordraht, die durch eine variable Spannungsquelle verbunden sind, wobei der Kollektor negativer ist als die Platte. Wenn Licht (oder andere EM-Strahlung) auf die Platte in der evakuierten Röhre trifft, können Elektronen ausgestoßen werden. Wenn die Energie der Elektronen in Elektronenvolt (eV) größer ist als der Potenzialunterschied zwischen der Platte und dem Draht in Volt, werden einige Elektronen auf dem Draht aufgefangen. Da die Elektronenenergie in eV gleich eV ist, wobei q die Elektronenladung und V die Potenzialdifferenz ist, kann die Elektronenenergie durch Einstellen der Verzögerungsspannung zwischen dem Draht und der Platte gemessen werden. Die Spannung, die die Elektronen daran hindert, den Draht zu erreichen, entspricht der Energie in eV. Wenn z. B. -3,00 V die Elektronen kaum aufhält, beträgt ihre Energie 3,00 eV. Die Anzahl der ausgestoßenen Elektronen lässt sich durch Messung des Stroms zwischen Draht und Platte bestimmen. Je mehr Licht, desto mehr Elektronen; mit einem kleinen Schaltkreis kann dieses Gerät als Lichtmesser verwendet werden.
Was wirklich wichtig am photoelektrischen Effekt ist, ist das, was Albert Einstein daraus ableitete. Einstein erkannte, dass es mehrere Eigenschaften des photoelektrischen Effekts gibt, die nur erklärt werden können, wenn die EM-Strahlung selbst quantisiert ist: Der scheinbar kontinuierliche Energiestrom einer EM-Welle besteht in Wirklichkeit aus Energiequanten, die Photonen genannt werden. In seiner Erklärung des photoelektrischen Effekts definierte Einstein eine quantisierte Einheit oder ein Quantum EM-Energie, das wir heute als Photon bezeichnen, mit einer Energie, die proportional zur Frequenz der EM-Strahlung ist. In Form einer Gleichung ist die Photonenenergie E = hf, wobei E die Energie eines Photons der Frequenz f und h die Plancksche Konstante ist. Diese revolutionäre Idee ähnelt der Planck’schen Quantisierung von Energiezuständen in Schwarzkörperoszillatoren, aber sie ist ganz anders. Es handelt sich um die Quantisierung der EM-Strahlung selbst. EM-Wellen bestehen aus Photonen und sind keine kontinuierlichen, glatten Wellen, wie in den vorangegangenen Kapiteln über Optik beschrieben. Ihre Energie wird in Klumpen absorbiert und emittiert, nicht kontinuierlich. Dies stimmt genau mit der Planckschen Quantisierung der Energieniveaus in Schwarzkörperoszillatoren überein, da diese Oszillatoren ihre Energie in Schritten von hf durch Absorption und Emission von Photonen mit E = hf erhöhen und verringern. Wir beobachten dies nicht mit unseren Augen, weil es in gewöhnlichen Lichtquellen so viele Photonen gibt, dass einzelne Photonen unbemerkt bleiben. (Siehe Abbildung 2.) Der nächste Abschnitt des Textes (Photonenenergien und das elektromagnetische Spektrum) ist einer Diskussion der Photonen und einiger ihrer Eigenschaften und Auswirkungen gewidmet. Für den Moment werden wir das Photonenkonzept verwenden, um den photoelektrischen Effekt zu erklären, ähnlich wie es Einstein tat.
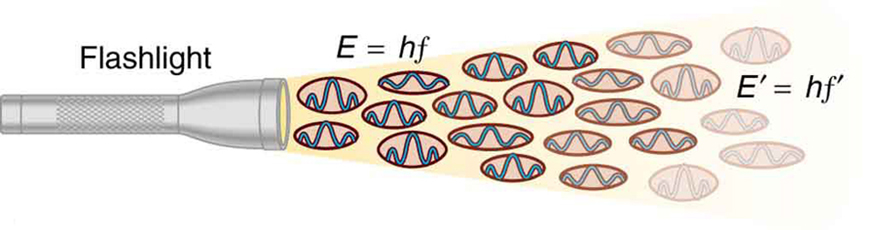
Abbildung 2. Eine EM-Welle der Frequenz f setzt sich aus Photonen, also einzelnen Quanten der EM-Strahlung, zusammen. Die Energie eines jeden Photons ist E = hf, wobei h die Plancksche Konstante und f die Frequenz der EM-Strahlung ist. Eine höhere Intensität bedeutet mehr Photonen pro Flächeneinheit. Die Taschenlampe sendet eine große Anzahl von Photonen mit vielen verschiedenen Frequenzen aus, so dass andere die Energie E′ = hf′ haben usw.
Der photoelektrische Effekt hat die unten beschriebenen Eigenschaften. Alle diese Eigenschaften stimmen mit der Vorstellung überein, dass einzelne Photonen der EM-Strahlung von einzelnen Elektronen in einem Material absorbiert werden, wobei das Elektron die Energie des Photons gewinnt. Einige dieser Eigenschaften sind mit der Vorstellung unvereinbar, dass EM-Strahlung eine einfache Welle ist. Betrachten wir der Einfachheit halber, was mit monochromatischer EM-Strahlung geschieht, bei der alle Photonen die gleiche Energie hf haben.
- Wenn wir die Frequenz der EM-Strahlung, die auf ein Material fällt, variieren, finden wir Folgendes: Für ein gegebenes Material gibt es eine Schwellenfrequenz f0 für die EM-Strahlung, unterhalb derer keine Elektronen herausgeschleudert werden, unabhängig von der Intensität. Einzelne Photonen wechselwirken mit einzelnen Elektronen. Wenn also die Photonenenergie zu gering ist, um ein Elektron wegzubrechen, werden keine Elektronen herausgeschleudert. Wäre die EM-Strahlung eine einfache Welle, könnte man durch Erhöhung der Intensität genügend Energie gewinnen.
- Sobald die EM-Strahlung auf ein Material fällt, werden die Elektronen ohne Verzögerung herausgeschleudert. Sobald ein einzelnes Photon mit einer ausreichend hohen Frequenz von einem einzelnen Elektron absorbiert wird, wird das Elektron ausgestoßen. Wäre die EM-Strahlung eine einfache Welle, würde es mehrere Minuten dauern, bis genügend Energie auf der Metalloberfläche deponiert ist, um ein Elektron auszustoßen.
- Die Anzahl der pro Zeiteinheit ausgestoßenen Elektronen ist proportional zur Intensität der EM-Strahlung und zu keiner anderen Eigenschaft. EM-Strahlung hoher Intensität besteht aus einer großen Anzahl von Photonen pro Flächeneinheit, wobei alle Photonen die gleiche charakteristische Energie hf haben.
- Wenn wir die Intensität der EM-Strahlung variieren und die Energie der ausgestoßenen Elektronen messen, finden wir Folgendes: Die maximale kinetische Energie der herausgeschleuderten Elektronen ist unabhängig von der Intensität der EM-Strahlung. Da es in einem Material so viele Elektronen gibt, ist es äußerst unwahrscheinlich, dass zwei Photonen gleichzeitig mit demselben Elektron wechselwirken und ihm dadurch mehr Energie verleihen. Stattdessen führt (wie in Punkt 3 oben erwähnt) eine höhere Intensität dazu, dass mehr Elektronen mit der gleichen Energie ausgestoßen werden. Wäre die EM-Strahlung eine einfache Welle, könnte eine höhere Intensität mehr Energie liefern, und es würden Elektronen mit höherer Energie ausgestoßen.
- Die kinetische Energie eines ausgestoßenen Elektrons ist gleich der Photonenenergie abzüglich der Bindungsenergie des Elektrons in dem betreffenden Material. Ein einzelnes Photon kann seine gesamte Energie an ein Elektron abgeben. Die Energie des Photons wird zum Teil dazu verwendet, das Elektron aus dem Material herauszulösen. Der Rest geht in die kinetische Energie des ausgestoßenen Elektrons ein. Die Gleichung lautet: KEe = hf – BE, wobei KEe die maximale kinetische Energie des ausgestoßenen Elektrons, hf die Energie des Photons und BE die Bindungsenergie des Elektrons an das jeweilige Material ist. (Diese Gleichung, die auf Einstein im Jahr 1905 zurückgeht, erklärt die Eigenschaften des photoelektrischen Effekts quantitativ. Ein einzelnes Photon der EM-Strahlung (anders geht es nicht) tritt mit einem einzelnen Elektron in Wechselwirkung und liefert dabei genügend Energie, BE, um es abzuspalten, wobei der Rest in kinetische Energie umgewandelt wird. Die Bindungsenergie ist BE = hf0, wobei f0 die Grenzfrequenz für das jeweilige Material ist. Abbildung 3 zeigt ein Diagramm der maximalen KEe in Abhängigkeit von der Frequenz der einfallenden EM-Strahlung, die auf ein bestimmtes Material fällt.
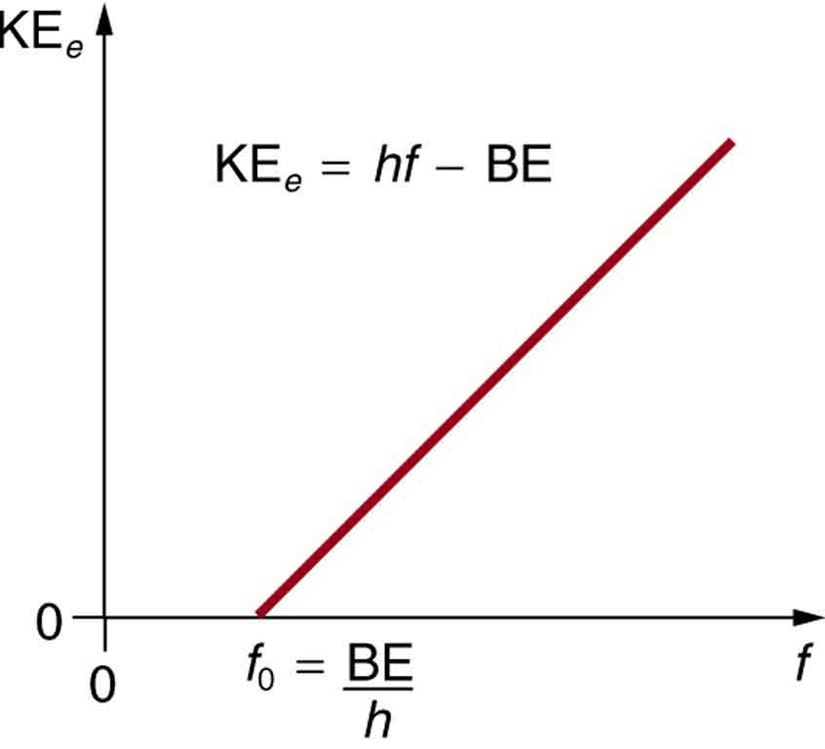
Abbildung 3. Photoelektrischer Effekt. Ein Diagramm der kinetischen Energie eines ausgeworfenen Elektrons, KEe, in Abhängigkeit von der Frequenz der auf ein bestimmtes Material auftreffenden EM-Strahlung. Es gibt eine Schwellenfrequenz, unterhalb derer keine Elektronen herausgeschleudert werden, weil das einzelne Photon, das mit einem einzelnen Elektron wechselwirkt, nicht genügend Energie hat, um es abzureißen. Oberhalb der Schwellenenergie nimmt KEe linear mit f zu, was der Gleichung KEe = hf – BE entspricht. Die Steigung dieser Linie ist h – die Daten können verwendet werden, um die Plancksche Konstante experimentell zu bestimmen. Einstein lieferte die erste erfolgreiche Erklärung für diese Daten, indem er die Idee der Photonen – Quanten der EM-Strahlung – vorschlug.
Einsteins Idee, dass EM-Strahlung gequantelt ist, war entscheidend für die Anfänge der Quantenmechanik. Es ist ein viel allgemeineres Konzept, als seine Erklärung des photoelektrischen Effekts vermuten lässt. Die gesamte EM-Strahlung kann auch in Form von Photonen modelliert werden, und die Eigenschaften der EM-Strahlung sind mit dieser Tatsache völlig vereinbar. (Wie wir im nächsten Abschnitt sehen werden, lassen sich viele Aspekte der EM-Strahlung, wie z. B. die Gefahren der ultravioletten (UV) Strahlung, nur durch die Eigenschaften von Photonen erklären). Einstein, der eher für die moderne Relativitätstheorie bekannt ist, legte 1905, im selben Jahr, in dem er seine erste Arbeit über die spezielle Relativitätstheorie veröffentlichte, einen wichtigen Grundstein für die Quantenmechanik. Seine Erklärung des photoelektrischen Effekts war die Grundlage für den Nobelpreis, der ihm 1921 verliehen wurde. Obwohl auch seine anderen Beiträge zur theoretischen Physik in dieser Auszeichnung gewürdigt wurden, wurden die spezielle und die allgemeine Relativitätstheorie nicht in vollem Umfang anerkannt, obwohl sie bis 1921 teilweise experimentell verifiziert worden waren. Obwohl dieser große Mann als Held verehrt wurde, erhielt er nie den Nobelpreis für sein berühmtestes Werk, die Relativitätstheorie.
Beispiel 1. Berechnung der Photonenenergie und des photoelektrischen Effekts: Ein violettes Licht
1. Wie hoch ist die Energie eines Photons von 420 nm violettem Licht in Joule und Elektronenvolt?
2. Wie hoch ist die maximale kinetische Energie von Elektronen, die durch 420 nm violettes Licht aus Kalzium herausgeschleudert werden, wenn man davon ausgeht, dass die Bindungsenergie (oder Arbeitsfunktion) von Elektronen für Kalziummetall 2,71 eV beträgt?
Strategie
Um Teil 1 zu lösen, beachten Sie, dass die Energie eines Photons durch E = hf gegeben ist. Sobald die Energie des Photons für Teil 2 berechnet ist, ist es eine einfache Anwendung von KEe = hf – BE, um die maximale kinetische Energie des ausgestoßenen Elektrons zu finden, da BE gegeben ist.
Lösung für Teil 1
Die Energie des Photons ist gegeben durch E = hf.
Da uns die Wellenlänge und nicht die Frequenz gegeben ist, lösen wir die bekannte Beziehung c = fλ für die Frequenz und erhalten f=\frac{c}{\lambda}\\.
Die Kombination dieser beiden Gleichungen ergibt die nützliche Beziehung E=\frac{hc}{\lambda}\\.
Setzt man nun die bekannten Werte ein, erhält man
\displaystyle{E}=\frac{\left(6.63\times10^{-34}\text{ J}\cdot\text{ s}\right)\left(3.00\times10^{8}\text{ m/s}\right)}{420\times10^{-9}\text{ m}}=4.74\times10^{-19}\text{ J}\\
Umgerechnet in eV ist die Energie des Photons
\displaystyle{E}=\left(4.47\times10^{-19}\text{ J}\right)\frac{1\text{ eV}}{1.6\times10^{-19}\text{ J}}=2.96\text{ eV}\
Lösung für Teil 2
Die Bestimmung der kinetischen Energie des ausgestoßenen Elektrons ist nun eine einfache Anwendung der Gleichung KEe = hf – BE. Setzt man die Photonenenergie und die Bindungsenergie ein, so erhält man KEe = hf – BE = 2,96 eV – 2,71 eV = 0,246 eV.
Diskussion
Die Energie dieses 420-nm-Photons violetten Lichts ist ein winziger Bruchteil eines Joule, und so ist es nicht verwunderlich, dass ein einzelnes Photon für uns nur schwer direkt wahrnehmbar ist – wir Menschen sind eher auf Energien in der Größenordnung von Joule eingestellt. Betrachtet man jedoch die Energie in Elektronenvolt, so kann man feststellen, dass dieses Photon genug Energie hat, um Atome und Moleküle zu beeinflussen. Ein DNA-Molekül kann beispielsweise mit einer Energie von etwa 1 eV gebrochen werden, und die typischen atomaren und molekularen Energien liegen in der Größenordnung von eV, so dass das UV-Photon in diesem Beispiel biologische Auswirkungen haben könnte. Das herausgeschleuderte Elektron (ein so genanntes Photoelektron) hat eine relativ geringe Energie und würde nicht weit reisen, außer in einem Vakuum. Das Elektron würde durch ein Bremspotenzial von nur 0,26 eV gestoppt werden. Wäre die Wellenlänge des Photons länger und seine Energie geringer als 2,71 eV, würde die Formel eine negative kinetische Energie ergeben, was nicht möglich ist. Das bedeutet einfach, dass die 420-nm-Photonen mit ihrer Energie von 2,96 eV nicht weit über der Frequenzschwelle liegen. Sie können selbst nachweisen, dass die Schwellenwellenlänge bei 459 nm (blaues Licht) liegt. Das bedeutet, dass ein Lichtmessgerät mit Kalziummetall für Wellenlängen, die länger als die des blauen Lichts sind, unempfindlich ist. Ein solcher Belichtungsmesser wäre z. B. für rotes Licht völlig unempfindlich.
PhET Explorations: Photoelektrischer Effekt
Sehen Sie, wie Licht Elektronen aus einem Metalltarget herausschlägt, und stellen Sie das Experiment nach, das die Quantenmechanik begründet hat.

Klicken Sie, um die Simulation herunterzuladen. Führen Sie die Simulation mit Java aus.
Zusammenfassung des Abschnitts
- Der photoelektrische Effekt ist der Prozess, bei dem EM-Strahlung Elektronen aus einem Material ausstößt.
- Einstein schlug vor, dass Photonen Quanten von EM-Strahlung mit der Energie E = hf sind, wobei f die Frequenz der Strahlung ist.
- Alle EM-Strahlung besteht aus Photonen. Wie Einstein erklärte, sind alle Eigenschaften des photoelektrischen Effekts auf die Wechselwirkung einzelner Photonen mit einzelnen Elektronen zurückzuführen.
- Die maximale kinetische Energie KEe der ausgestoßenen Elektronen (Photoelektronen) ist gegeben durch KEe = hf – BE, wobei hf die Photonenenergie und BE die Bindungsenergie (oder Arbeitsfunktion) des Elektrons an das jeweilige Material ist.
Konzeptuelle Fragen
- Ist sichtbares Licht die einzige Art von EM-Strahlung, die den photoelektrischen Effekt verursachen kann?
- Welche Aspekte des photoelektrischen Effekts können nicht ohne Photonen erklärt werden? Welche lassen sich ohne Photonen erklären? Sind letztere unvereinbar mit der Existenz von Photonen?
- Ist der photoelektrische Effekt eine direkte Folge des Wellencharakters der EM-Strahlung oder des Teilchencharakters der EM-Strahlung? Erläutern Sie kurz.
- Isolatoren (Nichtmetalle) haben einen höheren BE als Metalle, und es ist für Photonen schwieriger, Elektronen aus Isolatoren herauszulösen. Erläutere, wie dies mit den freien Ladungen in Metallen zusammenhängt, die sie zu guten Leitern machen.
- Wenn man ein Stück Metall in die Hand nimmt und schüttelt, das Elektronen enthält, die sich frei als Strom bewegen können, fallen keine Elektronen heraus. Wenn man aber das Metall erhitzt, können Elektronen herausgeschlagen werden. Erläutern Sie diese beiden Tatsachen in Bezug auf die Energiemenge und -verteilung beim Schütteln des Objekts im Vergleich zum Erwärmen.
Probleme & Übungen
- Welches ist die längste Wellenlänge der EM-Strahlung, die ein Photoelektron aus Silber herausschlagen kann, wenn die Bindungsenergie 4,73 eV beträgt? Liegt dies im sichtbaren Bereich?
- Bestimmen Sie die längste Wellenlänge des Photons, das ein Elektron aus Kalium ausstoßen kann, wenn die Bindungsenergie 2,24 eV beträgt. Handelt es sich dabei um sichtbare EM-Strahlung?
- Wie hoch ist die Bindungsenergie in eV von Elektronen in Magnesium, wenn die längste Wellenlänge des Photons, das Elektronen ausstoßen kann, 337 nm beträgt?
- Berechnen Sie die Bindungsenergie in eV von Elektronen in Aluminium, wenn die längste Wellenlänge des Photons, das Elektronen ausstoßen kann, 304 nm beträgt.
- Wie hoch ist die maximale kinetische Energie in eV von Elektronen, die durch 450-nm-EM-Strahlung aus Natriummetall herausgeschleudert werden, wenn die Bindungsenergie 2,28 eV beträgt?
- UV-Strahlung mit einer Wellenlänge von 120 nm fällt auf Goldmetall, an das Elektronen mit 4,82 eV gebunden sind. Wie groß ist die maximale kinetische Energie der ausgestoßenen Photoelektronen?
- Violettes Licht der Wellenlänge 400 nm stößt Elektronen mit einer maximalen kinetischen Energie von 0,860 eV aus Natriummetall aus. Wie hoch ist die Bindungsenergie von Elektronen an Natriummetall?
- UV-Strahlung mit einer Wellenlänge von 300 nm fällt auf Uranmetall und stößt Elektronen mit einer maximalen kinetischen Energie von 0,500 eV aus. Wie groß ist die Bindungsenergie von Elektronen an Uranmetall?
- (a) Welche Wellenlänge hat die EM-Strahlung, die 2,00-eV-Elektronen aus Kalziummetall herausschlägt, wenn die Bindungsenergie 2,71 eV beträgt? (b) Um welche Art von EM-Strahlung handelt es sich?
- Bestimmen Sie die Wellenlänge der Photonen, die 0,100-eV-Elektronen aus Kalium herausschlagen, wenn die Bindungsenergie 2,24 eV beträgt. Sind diese Photonen sichtbar?
- Wie hoch ist die maximale Geschwindigkeit von Elektronen, die von 80-nm-Photonen aus einem Material herausgeschleudert werden, wenn sie mit 4,73 eV an das Material gebunden sind?
- Photoelektronen aus einem Material mit einer Bindungsenergie von 2,71 eV werden von 420-nm-Photonen herausgeschleudert. Wie lange brauchen diese Elektronen nach dem Ausstoß, um 2,50 cm bis zu einem Nachweisgerät zurückzulegen?
- Ein Laser mit einer Leistung von 2,00 mW bei einer Wellenlänge von 400 nm wird auf Calciummetall projiziert. (a) Wie viele Elektronen werden pro Sekunde herausgeschlagen? (b) Welche Leistung wird von den Elektronen fortgetragen, wenn man davon ausgeht, dass die Bindungsenergie 2,71 eV beträgt?
- (a) Berechnen Sie die Anzahl der Photoelektronen pro Sekunde, die von einer 1,00 mm2 großen Fläche aus Natriummetall durch 500-nm-EM-Strahlung mit einer Intensität von 1,30 kW/m2 (die Intensität des Sonnenlichts über der Erdatmosphäre) ausgestoßen werden. (b) Wenn die Bindungsenergie 2,28 eV beträgt, welche Leistung wird dann von den Elektronen weggetragen? (c) Die Elektronen transportieren weniger Energie ab als die Photonen einbringen. Wohin geht die andere Energie? Wie kann sie zurückgewonnen werden?
- Unbegründete Ergebnisse. Rotes Licht mit einer Wellenlänge von 700 nm wird auf Magnesiummetall projiziert, an das Elektronen mit 3,68 eV gebunden sind. (a) Berechnen Sie mit KEe = hf – BE die kinetische Energie der ausgestoßenen Elektronen. (b) Was ist an diesem Ergebnis unvernünftig? (c) Welche Annahmen sind unvernünftig oder widersprüchlich?
- Unvernünftige Ergebnisse. (a) Wie hoch ist die Bindungsenergie von Elektronen an ein Material, aus dem 4,00-eV-Elektronen durch 400-nm-EM-Strahlung herausgeschleudert werden? (b) Was ist an diesem Ergebnis unvernünftig? (c) Welche Annahmen sind unvernünftig oder widersprüchlich?
Glossar
Photoelektrischer Effekt: das Phänomen, bei dem einige Materialien Elektronen ausstoßen, wenn sie mit Licht bestrahlt werden
Photon: ein Quantum oder Teilchen elektromagnetischer Strahlung
Photonenenergie: die Energiemenge, die ein Photon hat; E = hf
Bindungsenergie: auch Arbeitsfunktion genannt; die Energiemenge, die notwendig ist, um ein Elektron aus einem Material herauszuschleudern
Ausgewählte Lösungen zu Aufgaben & Übungen
1. 263 nm
3. 3,69 eV
5. 0,483 eV
7. 2,25 eV
9. (a) 264 nm; (b) Ultraviolett
11. 1,95 × 106 m/s
13. (a) 4,02 × 1015 s; (b) 0,256 mW
15. (a) -1,90 eV; (b) Negative kinetische Energie; (c) Dass die Elektronen frei geschlagen würden.
