Das Phasendiagramm von Wasser
Abbildung 11.23 „Zwei Versionen des Phasendiagramms von Wasser“ zeigt das Phasendiagramm von Wasser und veranschaulicht, dass der Tripelpunkt von Wasser bei 0,01°C und 0,00604 atm (4,59 mmHg) liegt. Der Tripelpunkt (273,16 K) ist weitaus reproduzierbarer als der Schmelzpunkt von Eis, der von der Menge der gelösten Luft und dem atmosphärischen Druck abhängt, und wird zur Definition der absoluten Temperaturskala (Kelvin) verwendet. Der Tripelpunkt stellt auch den niedrigsten Druck dar, bei dem eine flüssige Phase im Gleichgewicht mit einem Feststoff oder Dampf existieren kann. Bei einem Druck von weniger als 0,00604 atm schmilzt Eis also nicht zu einer Flüssigkeit, wenn die Temperatur steigt; der Feststoff sublimiert direkt zu Wasserdampf. Die Sublimation von Wasser bei niedriger Temperatur und niedrigem Druck kann zum „Gefriertrocknen“ von Lebensmitteln und Getränken verwendet werden. Das Lebensmittel oder Getränk wird zunächst auf Minustemperaturen abgekühlt und in einen Behälter gegeben, in dem der Druck unter 0,00604 atm gehalten wird. Dann, wenn die Temperatur erhöht wird, sublimiert das Wasser und hinterlässt die dehydrierten Lebensmittel (wie sie von Rucksacktouristen oder Astronauten verwendet werden) oder das pulverisierte Getränk (wie bei gefriergetrocknetem Kaffee).
Das Phasendiagramm für Wasser, das in Teil (b) in Abbildung 11.23 „Zwei Versionen des Phasendiagramms von Wasser“ dargestellt ist, zeigt die Grenze zwischen Eis und Wasser in einem erweiterten Maßstab. Die Schmelzkurve von Eis verläuft nach oben und leicht nach links und nicht nach oben und rechts wie in Abbildung 11.22 „Ein typisches Phasendiagramm für eine Substanz, die drei Phasen – fest, flüssig und gasförmig – und einen überkritischen Bereich aufweist“; das heißt, der Schmelzpunkt von Eis sinkt mit zunehmendem Druck; bei 100 MPa (987 atm) schmilzt Eis bei -9°C. Wasser verhält sich so, weil es eine der wenigen bekannten Substanzen ist, bei denen der kristalline Festkörper eine geringere Dichte als die Flüssigkeit aufweist (andere sind Antimon und Wismut). Erhöht man den Druck von Eis, das sich bei 0 °C und 1 atm im Gleichgewicht mit Wasser befindet, so werden einige der Moleküle enger zusammengedrückt, wodurch das Volumen der Probe abnimmt. Die Abnahme des Volumens (und die entsprechende Zunahme der Dichte) ist bei einem Feststoff oder einer Flüssigkeit geringer als bei einem Gas, aber sie reicht aus, um einen Teil des Eises zu schmelzen.
Abbildung 11.23 Zwei Versionen des Phasendiagramms von Wasser
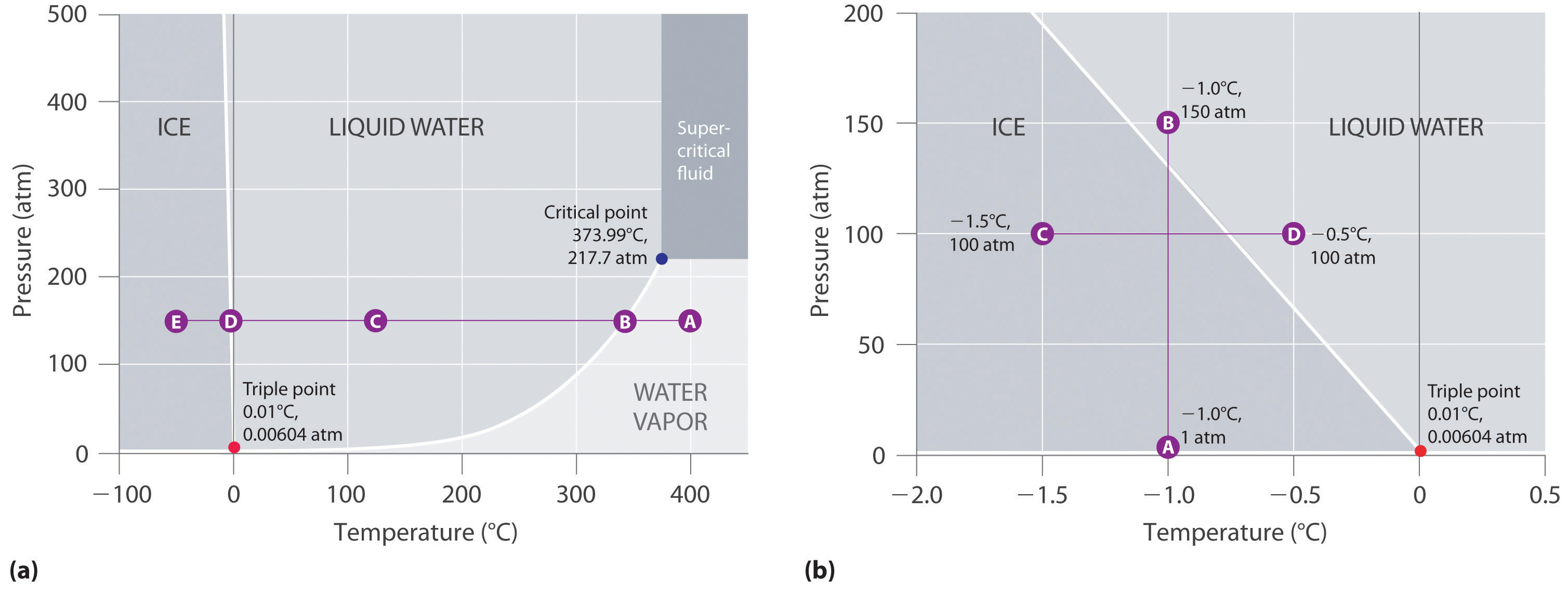
(a) In diesem Diagramm mit linearen Temperatur- und Druckachsen verläuft die Grenze zwischen Eis und flüssigem Wasser fast senkrecht. (b) Dieses Diagramm mit erweiterter Skala veranschaulicht die Abnahme des Schmelzpunkts mit zunehmendem Druck. (Die Buchstaben beziehen sich auf die in Beispiel 10 besprochenen Punkte.)
In Teil (b) in Abbildung 11.23 „Zwei Versionen des Phasendiagramms von Wasser“ befindet sich Punkt A bei P = 1 atm und T = -1,0°C im festen (Eis-)Bereich des Phasendiagramms. Steigt der Druck bei gleichbleibender Temperatur auf 150 atm, so verläuft die Linie von Punkt A über die Eis/Wasser-Grenze zu Punkt B, der im Bereich des flüssigen Wassers liegt. Folglich schmilzt Eis bei -1,0 °C, wenn ein Druck von 150 atm angewendet wird. Wir haben bereits darauf hingewiesen, dass die Druckabhängigkeit des Schmelzpunkts von Wasser von entscheidender Bedeutung ist. Wenn die Grenze zwischen fest und flüssig im Phasendiagramm von Wasser schräg nach oben und rechts statt nach links verlaufen würde, wäre Eis dichter als Wasser, Eiswürfel würden sinken, Wasserleitungen würden nicht platzen, wenn sie einfrieren, und Frostschutzmittel wäre in Automotoren überflüssig.
Bis vor kurzem wurde in vielen Lehrbüchern beschrieben, dass Schlittschuhlaufen möglich ist, weil der von der Kufe des Schlittschuhläufers erzeugte Druck hoch genug ist, um das Eis unter der Kufe zu schmelzen, wodurch eine Schmierschicht aus flüssigem Wasser entsteht, die das Gleiten der Kufe über das Eis ermöglicht. Obwohl diese Erklärung intuitiv befriedigend ist, ist sie falsch, wie wir durch eine einfache Berechnung zeigen können. Aus Kapitel 10 „Gase“ wissen wir, dass der Druck (P) die Kraft (F) ist, die pro Flächeneinheit (A) ausgeübt wird:
Gleichung 11.4
P = F A
Um den Druck zu berechnen, den ein Schlittschuhläufer auf das Eis ausübt, müssen wir nur die ausgeübte Kraft und die Fläche der Schlittschuhkufe berechnen. Wenn wir von einem 75,0 kg schweren Schlittschuhläufer ausgehen, dann ist die Kraft, die der Schlittschuhläufer aufgrund der Schwerkraft auf das Eis ausübt
Gleichung 11.5
F = mg
wobei m die Masse und g die Erdbeschleunigung (9,81 m/s2) ist. Die Kraft ist also
Gleichung 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Wenn wir annehmen, dass die Schlittschuhkufen 2.0 mm breit und 25 cm lang sind, dann ist die Fläche der Unterseite jeder Kufe
Gleichung 11.7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Gleitet der Läufer auf einem Fuß, so ist der auf das Eis ausgeübte Druck
Gleichung 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
Der Druck ist viel geringer als der Druck, der erforderlich ist, um den Schmelzpunkt von Eis auch nur um 1 °C zu senken, und die Erfahrung zeigt, dass man auch bei Temperaturen weit unter dem Gefrierpunkt Schlittschuh laufen kann. Das druckbedingte Schmelzen des Eises kann also nicht die geringe Reibung erklären, die Schlittschuhläufern (und Hockeypucks) das Gleiten ermöglicht. Jüngste Forschungen zeigen, dass die Oberfläche des Eises, wo die geordnete Anordnung der Wassermoleküle auf die Luft trifft, aus einer oder mehreren Schichten fast flüssigen Wassers besteht. Diese Schichten scheinen zusammen mit dem Schmelzen, das durch die Reibung beim Vorwärtsschieben des Schlittschuhläufers entsteht, sowohl für die Leichtigkeit des Gleitens als auch für die Tatsache verantwortlich zu sein, dass das Schlittschuhlaufen unterhalb von etwa -7°C schwieriger wird, wenn die Anzahl der schmierenden Oberflächenwasserschichten abnimmt.
