In diesem Abschnitt werden wir uns mit Mengenoperationen und Notationen vertraut machen, so dass wir diese Konzepte sowohl auf Zähl- als auch auf Wahrscheinlichkeitsprobleme anwenden können. Wir beginnen mit der Definition einiger Begriffe.
Eine Menge ist eine Sammlung von Objekten, und ihre Mitglieder werden die Elemente der Menge genannt. Wir benennen die Menge mit Großbuchstaben und schließen ihre Mitglieder in geschweifte Klammern ein. Angenommen, wir müssen die Mitglieder des Schachclubs auflisten. Wir verwenden die folgende Mengenschreibweise:
C ={Ken, Bob, Tran, Shanti, Eric}
Eine Menge, die keine Mitglieder hat, nennt man eine leere Menge. Die leere Menge wird mit dem Symbol Ø bezeichnet.
Zwei Mengen sind gleich, wenn sie die gleichen Elemente haben.
Eine Menge A ist eine Teilmenge einer Menge B, wenn jedes Mitglied von A auch ein Mitglied von B ist.
Angenommen, C = {Al, Bob, Chris, David, Ed} und A = {Bob, David}. Dann ist A eine Teilmenge von C, geschrieben als 
.
Jede Menge ist eine Teilmenge von sich selbst, und die leere Menge ist eine Teilmenge von jeder Menge.
Vereinigung zweier Mengen
Sind A und B zwei Mengen, dann ist die Vereinigung von A und B, geschrieben als 
, die Menge aller Elemente, die entweder in A oder in B oder sowohl in A als auch in B sind.
Schnittmenge zweier Mengen
Sind A und B zwei Mengen, dann ist die Schnittmenge von A und B, geschrieben 
, die Menge aller Elemente, die beiden Mengen A und B gemeinsam sind.
Eine Universalmenge U ist die Menge, die aus allen betrachteten Elementen besteht.
Komplement einer Menge
Ist A eine beliebige Menge, so ist das Komplement der Menge A, geschrieben 
, die Menge, die aus Elementen der Universalmenge U besteht, die nicht in A enthalten sind.
Disjunkte Mengen
Zwei Mengen A und B heißen disjunkte Mengen, wenn ihre Schnittmenge eine leere Menge ist.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {Orange, Grün, Indigo, Violett}Zum besseren Verständnis nehmen wir an, dass die Universalmenge U die Farben des Spektrums und P die Primärfarben darstellt, dann stellt die Farben des Spektrums dar, die keine Primärfarben sind.
.
= {rot, gelb, blau, grün}
= {orange, indigo, violett}
= {rot, gelb, blau, violett} = {violett}Venn-Diagramme
Wir verwenden heute Venn-Diagramme, um die Beziehungen zwischen Mengen zu veranschaulichen. In den späten 1800er Jahren entwickelte ein englischer Logiker namens John Venn eine Methode zur Darstellung von Beziehungen zwischen Mengen. Er stellte diese Beziehungen mithilfe von Diagrammen dar, die heute als Venn-Diagramme bekannt sind. Ein Venn-Diagramm stellt eine Menge als das Innere eines Kreises dar. Oft werden zwei oder mehr Kreise von einem Rechteck umschlossen, wobei das Rechteck die Gesamtmenge darstellt. Die Veranschaulichung einer Schnittmenge oder Vereinigung einer Menge ist einfach. In diesem Abschnitt werden wir hauptsächlich Venn-Diagramme verwenden, um verschiedene Mengen zu sortieren und Objekte zu zählen.
|
(a) |
(b) |
(c) |
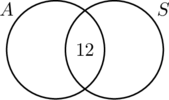
Weil 30 Personen Autos mit Automatikgetriebe fahren, muss der Kreis A 30 Elemente enthalten. Das bedeutet x + 12 = 30 oder x = 18. Da 20 Personen Autos mit normalem Getriebe fuhren, muss der Kreis B 20 Elemente enthalten, d. h. y + 12 = 20, was wiederum y = 8 ergibt.
Nachdem nun alle Informationen geordnet sind, lässt sich aus dem Diagramm leicht ablesen, dass 18 Personen nur Autos mit Automatikgetriebe fuhren, 12 Personen beide Arten von Autos fuhren und 8 nur Autos mit normalem Getriebe fuhren. Daher haben 18 + 12 + 8 = 38 Personen an der Umfrage teilgenommen.
|
(a) |
(b) |
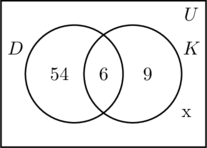
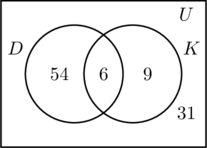
Wir füllen die drei Regionen, die mit den Mengen D und K verbunden sind, auf die gleiche Weise wie zuvor. Da 100 Personen an der Umfrage teilgenommen haben, muss das Rechteck, das die Universalmenge U darstellt, 100 Objekte enthalten. x steht für die Personen in der Universalmenge, die weder in der Menge D noch in K sind. Das bedeutet 54 + 6 + 9 + x = 100, oder x = 31.
Daher gibt es 31 Personen in der Umfrage, die keinen der beiden Orte besucht haben.
- 50 joggen, 30 schwimmen und 35 radfahren
- 14 joggen und schwimmen
- 7 schwimmen und radfahren
- 9 joggen und radfahren
- 3 Personen nehmen an allen drei Aktivitäten teil
Lösung
|
(a) |
(b) |
(c) |
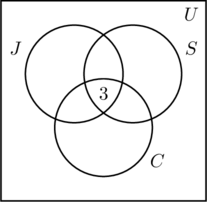
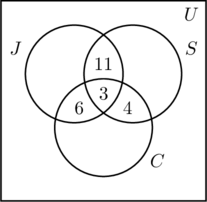
Wir setzen eine 3 in den innersten Bereich von Abbildung (a), weil sie die Anzahl der Personen darstellt, die an allen drei Aktivitäten teilnehmen. Als nächstes berechnen wir x, y und z.
- Da 14 Personen joggen und schwimmen, ist x +3 = 14, oder x = 11.
- Die Tatsache, dass 9 Personen joggen und Rad fahren, ergibt y + 3 = 9 oder y = 6.
- Da 7 Personen schwimmen und Rad fahren, ergibt sich z + 3 = 7 oder z = 4.
- Diese Informationen sind in Abbildung (b) dargestellt.
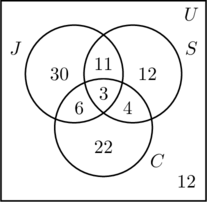
- Da 50 Personen joggen, ist m + 11 + 6 + 3 = 50 oder m = 30.
- 30 Personen schwimmen, also n + 11 + 4 + 3 = 30, oder n = 12.
- 35 Personen fahren Rad, also p + 6 + 4 + 3 = 35, oder p = 22.
- Wenn man alle Einträge in allen drei Gruppen addiert, erhält man eine Summe von 88. Da 100 Personen befragt wurden, ist die Zahl innerhalb der Universalmenge, aber außerhalb aller drei Mengen 100 – 88, also 12.
- In Abbildung (c) sind die Informationen sortiert, und die Fragen können leicht beantwortet werden.
Übungsfragen
1. Sei die Universalmenge U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h}, und W = {a, c, e, g, i}. Gib die Mitglieder der folgenden Mengen an:
a. 
b. 
2. Betrachte die folgenden Mengen: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, Influenza, Norovirus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella}, und C = {SARS, Listeria, Tuberkulose, H5N1, Salmonella, HIV, COVID-19}. Nenne die Mitglieder der folgenden Gruppen:
a. 
b. 
3. Eine Umfrage unter Sportlern ergab, dass bei leichten Schmerzen 30 Aspirin, 50 Ibuprofen und 15 beides verwenden. Alle befragten Sportler nahmen mindestens eines der beiden Schmerzmittel ein. Wie viele Sportler wurden befragt?
4. In einer Studie mit 150 High-School-Schülern gaben 25 an, eine frühere Gehirnerschütterung oder Kopfverletzung erlitten zu haben, 52 berichteten über psychische Erkrankungen, und 15 berichteten über beide Folgen. Wie viele Schüler gaben keines der beiden Ergebnisse an?
5. Eine Umfrage unter 100 Studenten der Ryerson University ergab, dass 50 ein Netflix-Abonnement haben, 40 ein Amazon Prime-Abonnement und 30 ein Disney+-Abonnement. Von diesen haben 15 sowohl Netflix als auch Amazon Prime abonniert, 10 sowohl Amazon Prime als auch Disney+, 10 sowohl Netflix als auch Disney+, und 5 haben alle drei Abonnements. Zeichnen Sie ein Venn-Diagramm und bestimmen Sie Folgendes:
a. Die Anzahl der Schüler, die Amazon Prime abonniert haben, aber nicht die beiden anderen Streaming-Dienste.
b. Die Anzahl der Schüler, die Netflix oder Amazon Prime abonniert haben, aber nicht Disney+.
c. Die Anzahl der Schüler, die keinen dieser Dienste abonniert haben.