MATH 1314: College Algebra

Wir wissen, wie man die Quadratwurzel aus jeder positiven reellen Zahl ziehen kann. Auf ähnliche Weise können wir die Quadratwurzel aus einer negativen Zahl ziehen. Der Unterschied ist, dass die Wurzel nicht real ist. Wenn der Wert des Radikanden negativ ist, nennt man die Wurzel eine imaginäre Zahl. Die imaginäre Zahl i ist definiert als die Quadratwurzel aus der negativen Zahl 1.

Wenn man also die Eigenschaften der Radikale benutzt,

Wir können die Quadratwurzel jeder negativen Zahl als ein Vielfaches von i schreiben. Betrachten wir die Quadratwurzel aus -25.

Wir verwenden 5i und nicht -\text{5}i\\, weil die Hauptwurzel von 25 die positive Wurzel ist.

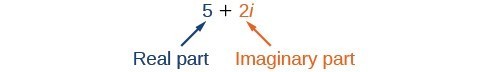
Abbildung 1

Eine komplexe Zahl ist die Summe aus einer reellen Zahl und einer imaginären Zahl. Eine komplexe Zahl wird in der Standardform ausgedrückt, indem man a + bi schreibt, wobei a der Realteil und bi der Imaginärteil ist. Zum Beispiel ist 5+2i\\ eine komplexe Zahl. Das Gleiche gilt für 3+4\sqrt{3}i\\.

Imaginäre Zahlen unterscheiden sich von reellen Zahlen, weil eine quadrierte imaginäre Zahl eine negative reelle Zahl ergibt. Zur Erinnerung: Wenn eine positive reelle Zahl quadriert wird, ist das Ergebnis eine positive reelle Zahl und wenn eine negative reelle Zahl quadriert wird, ist das Ergebnis wiederum eine positive reelle Zahl. Komplexe Zahlen sind eine Kombination aus realen und imaginären Zahlen.