Gruppe

Eine Gruppe ist eine endliche oder unendliche Menge von Elementen zusammen mit einer binären Operation (der sogenannten Gruppenoperation), die zusammen die vier grundlegenden Eigenschaften der Geschlossenheit, der Assoziativität, der Identitätseigenschaft und der inversen Eigenschaft erfüllen. Die Operation, in Bezug auf die eine Gruppe definiert ist, wird oft als „Gruppenoperation“ bezeichnet, und man sagt, eine Menge sei eine Gruppe „unter“ dieser Operation. Die Elemente , , , … mit der binären Operation zwischen und , bezeichnet als , bilden eine Gruppe, wenn

1. Schluss: Wenn und zwei Elemente in sind, dann ist das Produkt auch in .

2. Assoziativität: Die definierte Multiplikation ist assoziativ, d.h. für alle , .

3. Identität: Es gibt ein Identitätselement (auch bekannt als 1, oder ), so dass für jedes Element .

4. Inverse: Zu jedem Element muss es einen Kehrwert (auch Kehrwert genannt) geben. Daher enthält die Menge für jedes Element von ein Element , so dass .

Eine Gruppe ist ein Monoid, bei dem jedes Element invertierbar ist.

Eine Gruppe muss mindestens ein Element enthalten, wobei die einzige (bis zum Isomorphismus) Einzelelementgruppe als Trivialgruppe bezeichnet wird.

Die Lehre von den Gruppen wird als Gruppentheorie bezeichnet. Wenn es eine endliche Anzahl von Elementen gibt, nennt man die Gruppe eine endliche Gruppe, und die Anzahl der Elemente wird als die Gruppenordnung der Gruppe bezeichnet. Eine Teilmenge einer Gruppe, die unter der Gruppenoperation und der umgekehrten Operation geschlossen ist, wird Untergruppe genannt. Untergruppen sind ebenfalls Gruppen, und viele häufig vorkommende Gruppen sind in der Tat spezielle Untergruppen einer allgemeineren größeren Gruppe.

Ein grundlegendes Beispiel für eine endliche Gruppe ist die symmetrische Gruppe , die die Gruppe der Permutationen (oder „unter Permutation“) von Objekten ist. Die einfachste unendliche Gruppe ist die Menge der ganzen Zahlen unter gewöhnlicher Addition. Für kontinuierliche Gruppen kann man die reellen Zahlen oder die Menge der invertierbaren Matrizen betrachten. Die letzten beiden sind Beispiele für Lie-Gruppen.

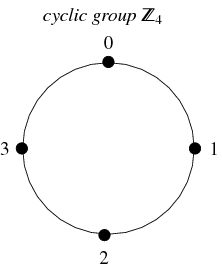
Eine sehr häufige Art von Gruppen sind die zyklischen Gruppen. Diese Gruppe ist isomorph zur Gruppe der ganzen Zahlen (modulo ), wird als , oder bezeichnet und ist für jede ganze Zahl definiert. Sie ist geschlossen unter Addition, assoziativ und hat eindeutige Inverse. Die Zahlen von 0 bis stellen ihre Elemente dar, wobei das Identitätselement durch 0 und die Inverse von durch dargestellt wird.

Eine Abbildung zwischen zwei Gruppen, die die Identität und die Gruppenoperation bewahrt, heißt Homomorphismus. Wenn ein Homomorphismus eine Umkehrung hat, die ebenfalls ein Homomorphismus ist, dann nennt man ihn einen Isomorphismus und die beiden Gruppen werden isomorph genannt. Zwei Gruppen, die zueinander isomorph sind, gelten als „gleich“, wenn man sie als abstrakte Gruppen betrachtet. Zum Beispiel ist die unten abgebildete Gruppe der Drehungen eines Quadrats die zyklische Gruppe .

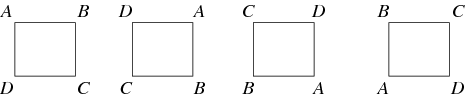
Im Allgemeinen handelt es sich um eine Gruppenaktion, wenn eine Gruppe auf eine Menge einwirkt und deren Elemente permutiert, so dass die Abbildung der Gruppe auf die Permutationsgruppe der Menge ein Homomorphismus ist. Zum Beispiel sind die Drehungen eines Quadrats eine Untergruppe der Permutationen seiner Ecken. Eine wichtige Gruppenaktion für jede Gruppe ist ihre Aktion auf sich selbst durch Konjugation. Dies sind nur einige der möglichen Gruppenautomorphismen. Eine andere wichtige Art von Gruppenwirkung ist eine Gruppendarstellung, bei der die Gruppe durch invertierbare lineare Abbildungen auf einen Vektorraum wirkt. Wenn das Feld des Vektorraums die komplexen Zahlen sind, wird eine Darstellung manchmal als CG-Modul bezeichnet.

Gruppenaktionen und insbesondere Darstellungen sind sehr wichtig für Anwendungen, nicht nur in der Gruppentheorie, sondern auch in der Physik und Chemie. Da man sich eine Gruppe als abstraktes mathematisches Objekt vorstellen kann, kann ein und dieselbe Gruppe in verschiedenen Kontexten auftreten. Es ist daher sinnvoll, eine Darstellung der Gruppe als eine bestimmte Verkörperung der Gruppe zu betrachten, die auch andere Darstellungen haben kann. Eine irreduzible Darstellung einer Gruppe ist eine Darstellung, für die es keine unitäre Transformation gibt, die die Darstellungsmatrix in die Form einer Blockdiagonale umwandelt. Die irreduziblen Darstellungen haben eine Reihe bemerkenswerter Eigenschaften, die im Satz von der Orthogonalität der Gruppe formuliert sind.