Wald-test: Definition, eksempler, hvordan man udfører testen

Hypotesetestning > Wald-test

Hvad er Wald-testet?

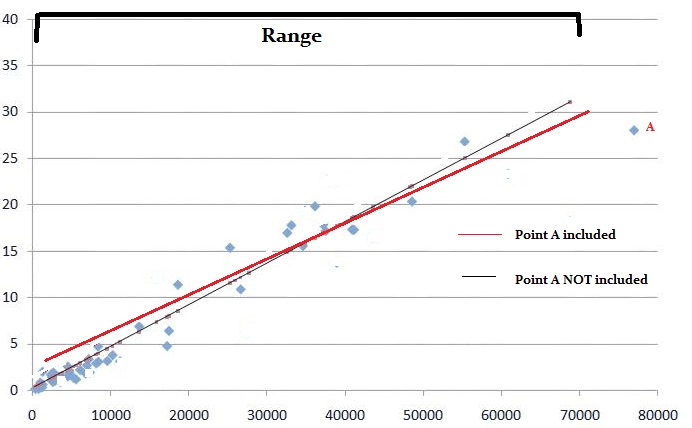
Wald-testen kan fortælle dig, hvilke modelvariabler der bidrager med noget signifikant.

Wald-testen (også kaldet Wald Chi-Squared-test) er en måde at finde ud af, om forklarende variabler i en model er signifikante. “Signifikant” betyder, at de bidrager med noget til modellen; variabler, der ikke bidrager med noget, kan slettes uden at påvirke modellen på nogen meningsfuld måde. Testen kan bruges til et væld af forskellige modeller, herunder modeller med binære variabler eller kontinuerlige variabler.
Nulhypotesen for testen er: en parameter = en værdi. Du kan f.eks. undersøge, om vægten påvirkes af at spise junkfood to gange om ugen. “Vægt” ville være din parameter. Værdien kunne være nul (hvilket indikerer, at du ikke tror, at vægten påvirkes af at spise junkfood). Hvis nulhypotesen forkastes, tyder det på, at de pågældende variabler kan fjernes, uden at det skader modellens tilpasning meget.

• Hvis Wald-testen viser, at parametrene for visse forklarende variabler er nul, kan du fjerne de pågældende variabler fra modellen.
• Hvis testen viser, at parametrene ikke er nul, bør du medtage variablerne i modellen.

Den Wald-test omtales normalt i form af chi-kvadrat, fordi stikprøvefordelingen (efterhånden som n nærmer sig uendelig) normalt er kendt. Denne variant af testen kaldes undertiden Wald-chi-kvadrat-testen for at skelne den fra Wald Log-Linear Chi-Square-testen, som er en ikke-parametrisk variant baseret på log-oddsratioerne.

Sammenligning med andre test

Wald-testen er en grov tilnærmelse af Likelihood Ratio-testen. Du kan dog køre den med en enkelt model (LR-testen kræver mindst to). Den er også mere bredt anvendelig end LRT: ofte kan du køre en Wald-test i situationer, hvor ingen anden test kan køres.

For store værdier af n svarer Wald-testen nogenlunde til t-testen; begge test vil forkaste de samme værdier for store stikprøvestørrelser. Wald-, LRT- og Lagrange-multiplikator-testen er alle ækvivalente, når stikprøvestørrelserne nærmer sig uendelig (kaldet “asymptotisk ækvivalente”). Stikprøver af en endelig størrelse, især mindre stikprøver, vil dog sandsynligvis give meget forskellige resultater.

Agresti (1990) foreslår, at du bør bruge LRT-testen i stedet for Wald-testen ved små stikprøvestørrelser, eller hvis parametrene er store. En “lille” stikprøvestørrelse er under ca. 30.

Afprøvning af testen

Har du brug for hjælp til et lektiehjælpsspørgsmål? Tjek vores vejledningsside!

Formlen for Wald-teststatistikken er: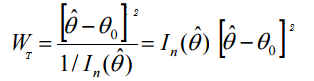

Hvor:

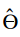• = Maximum Likelihood Estimator (MLE),
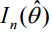• = forventet Fisher-information (evalueret ved MLE).

Helt grundlæggende ser testen efter forskelle: Θ0 – Θ. De generelle trin er:

1. Find MLE.
2. Find den forventede Fisher-information.
3. Evaluer Fisher-informationen ved MLE.

Med kombinationen af MLE og Fisher-information er Wald-testen meget kompleks at arbejde med, og den beregnes normalt ikke i hånden. Mange softwareprogrammer kan køre testen.

• Stata: Brug kommandoen test.
• R: Se WALD-testinstruktioner for R (download en PDF) fra University of Toronto.
• SAS: Brug TEST-erklæringen. WALD er standard, hvis der ikke er angivet nogen test.

Reference:
Agresti A. (1990) Categorical Data Analysis. John Wiley and Sons, New York.

——————————————————————————

Har du brug for hjælp til et spørgsmål om lektier eller en prøve? Med Chegg Study kan du få trin-for-trin-løsninger på dine spørgsmål fra en ekspert på området. Dine første 30 minutter med en Chegg-underviser er gratis!