
Pythagoras af Samos (ca.570-495 BCE)
Biografi – Hvem var Pythagoras
Det hævdes nogle gange, at vi skylder den rene matematik til Pythagoras, og han kaldes ofte den første “ægte” matematiker. Men selv om hans bidrag tydeligvis var vigtigt, er han ikke desto mindre fortsat en kontroversiel figur.
Han efterlod sig ikke selv nogen matematiske skrifter, og meget af det, vi ved om pythagoræisk tænkning, kommer til os fra Philolaus’ og andre senere pythagoræiske lærdes skrifter. Faktisk er det på ingen måde klart, om mange (eller overhovedet nogen) af de sætninger, der tilskrives ham, faktisk blev løst af Pythagoras personligt eller af hans tilhængere.
Den skole, han etablerede i Croton i Syditalien omkring 530 f.v.t., var kernen i en ret bizar pythagoræisk sekt. Selv om den pythagoræiske tankegang i høj grad var domineret af matematik, var den også dybt mystisk, og Pythagoras pålagde alle medlemmerne af sin skole sine kvasireligiøse filosofier, streng vegetarisme, fælles levevis, hemmelige ritualer og mærkelige regler (herunder bizarre og tilsyneladende tilfældige påbud om aldrig at tisse mod solen, aldrig at gifte sig med en kvinde, der bærer guldsmykker, aldrig at passere et æsel, der ligger på gaden, aldrig at spise eller blot røre ved sorte fava-bønner osv.
Medlemmerne blev delt op i “mathematikoi” (eller “lærende”), som udvidede og udviklede det mere matematiske og videnskabelige arbejde, som Pythagoras selv begyndte, og “akousmatikoi” (eller “lyttere”), som fokuserede på de mere religiøse og rituelle aspekter af hans lære. Der var altid en vis grad af gnidninger mellem de to grupper, og til sidst blev sekten indblandet i nogle voldsomme lokale kampe og spredte sig i sidste ende. Der opstod en vrede mod pythagoræernes hemmelighedsfuldhed og eksklusivitet, og i 460 f.Kr. blev alle deres mødesteder brændt og ødelagt, og mindst 50 medlemmer blev dræbt alene i Croton.
Det overordnede diktum i Pythagoras’ skole var “Alt er tal” eller “Gud er tal”, og pythagoræerne praktiserede i praksis en slags numerologi eller taldyrkelse, og de anså hvert tal for at have sin egen karakter og betydning. For eksempel var tallet et generatoren for alle tal; to repræsenterede mening; tre, harmoni; fire, retfærdighed; fem, ægteskab; seks, skabelse; syv, de syv planeter eller “vandrende stjerner”; osv. Ulige tal blev opfattet som kvindelige og lige tal som mandlige.
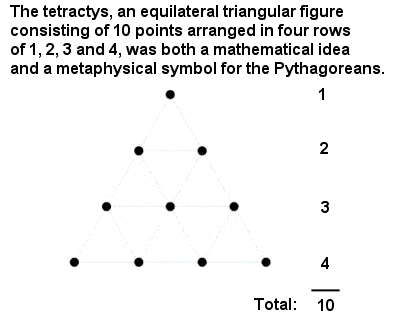
Den pythagoræiske Tetractys
Det helligste tal af alle var “Tetractys” eller ti, et trekantet tal, der består af summen af en, to, tre og fire. Det er en stor hyldest til pythagoræernes intellektuelle præstationer, at de udledte tallet 10’s særlige plads fra et abstrakt matematisk argument snarere end fra noget så banalt som at tælle fingrene på to hænder.
Pythagoras og hans skole – samt en håndfuld andre matematikere i det antikke Grækenland – var imidlertid i høj grad ansvarlig for at indføre en mere stringent matematik end det, der var gået forud, og som byggede ud fra første principper ved hjælp af aksiomer og logik. Før Pythagoras havde geometri f.eks. blot været en samling regler, der var udledt af empiriske målinger.
Pythagoras opdagede, at man kunne konstruere et fuldstændigt matematiksystem, hvor geometriske elementer svarede til tal, og hvor hele tal og deres forhold var alt, hvad der var nødvendigt for at etablere et helt system af logik og sandhed.
Den pythagoræiske sætning
Han huskes især for det, der er blevet kendt som Pythagoras’ sætning (eller den pythagoræiske sætning): at for enhver retvinklet trekant er kvadratet på længden af hypotenusen (den længste side, modsat den rette vinkel) lig med summen af kvadratet på de to andre sider (eller “ben”).
Skrevet som en ligning: a2 + b2 = c2.
Hvad Pythagoras og hans tilhængere ikke var klar over, er, at dette også gælder for enhver form: Således er arealet af en femkant på hypotenusen lig med summen af femkanterne på de to andre sider, ligesom det er tilfældet for en halvcirkel eller enhver anden regelmæssig (eller endog uregelmæssig() form.
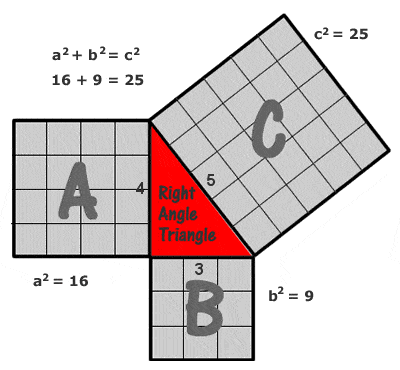
Pythagoras’ (Pythagoras’) sætning
Det enkleste og mest almindeligt citerede eksempel på en pythagoræisk trekant er en trekant med siderne på 3, 4 og 5 enheder (32 + 42 = 52, som det kan ses ved at tegne et gitter af enhedsfirkanter på hver side som i diagrammet til højre), men der findes et potentielt uendeligt antal andre hele “pythagoræiske trekanter”, begyndende med (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41) osv. Det skal dog bemærkes, at (6, 8, 10) ikke er det, man kalder en “primitiv” pythagoræisk trippel, da det blot er et multiplum af (3, 4, 5).
Pythagoras’ sætning og egenskaberne ved retvinklede trekanter synes at være den ældste og mest udbredte matematiske udvikling efter den grundlæggende aritmetik og geometri, og den blev berørt i nogle af de ældste matematiske tekster fra Babylon og Egypten, der stammer fra over tusind år tidligere. Et af de enkleste beviser stammer fra det gamle Kina og stammer sandsynligvis fra et godt stykke tid før Pythagoras’ fødsel. Det var dog Pythagoras, der gav sætningen sin endelige form, selv om det ikke er klart, om Pythagoras selv beviste den endeligt eller blot beskrev den. Under alle omstændigheder er det blevet et af de mest kendte af alle matematiske sætninger, og der findes nu op mod 400 forskellige beviser, nogle geometriske, nogle algebraiske, nogle med avancerede differentialligninger osv.
Det blev dog hurtigt klart, at der også var mulighed for ikke-integrale løsninger, således at en ligebenet trekant med siderne 1, 1 og √2 f.eks. også har en ret vinkel, som babylonierne havde opdaget århundreder tidligere. Da Pythagoras’ elev Hippasus imidlertid forsøgte at beregne værdien af √2, fandt han ud af, at det ikke var muligt at udtrykke den som en brøk, hvilket indikerede den potentielle eksistens af en helt ny verden af tal, nemlig de irrationelle tal (tal, der ikke kan udtrykkes som simple brøker af hele tal). Denne opdagelse slog temmelig meget den elegante matematiske verden, som Pythagoras og hans tilhængere havde bygget op, i stykker, og eksistensen af et tal, der ikke kunne udtrykkes som forholdet mellem to af Guds skabninger (sådan som de tænkte på de hele tal), bragte hele kultens trossystem i fare.
Den stakkels Hippasus blev tilsyneladende druknet af de hemmelighedsfulde pythagoræere for at have udsendt denne vigtige opdagelse til omverdenen. Men udskiftningen af ideen om de hele tals guddommelighed med det rigere begreb om kontinuummet var en væsentlig udvikling i matematikken. Det markerede den egentlige fødsel af den græske geometri, der beskæftiger sig med linjer og planer og vinkler, som alle er kontinuerlige og ikke diskrete.
Men blandt sine andre resultater inden for geometri indså Pythagoras (eller i det mindste hans efterfølgere, pythagoræerne) også, at summen af vinklerne i en trekant er lig med to rette vinkler (180°), og sandsynligvis også den generalisering, der fastslår, at summen af de indvendige vinkler i en polygon med n sider er lig med (2n – 4) rette vinkler, og at summen af de udvendige vinkler er lig med 4 rette vinkler. De var i stand til at konstruere figurer med et givet areal og til at anvende simpel geometrisk algebra, f.eks. til at løse ligninger som a(a – x) = x2 med geometriske midler.
Pythagoræerne etablerede også grundlaget for talteorien med deres undersøgelser af trekantede, kvadratiske og også perfekte tal (tal, der er summen af deres divisorer). De opdagede flere nye egenskaber ved kvadratiske tal, f.eks. at kvadratet på et tal n er lig med summen af de første n ulige tal (f.eks. 42 = 16 = 1 + 3 + 5 + 7). De opdagede også mindst det første par af amicable tal, 220 og 284 (amicable tal er par af tal, for hvilke summen af divisorerne af det ene tal er lig med det andet tal, f.eks. er de egentlige divisorer af 220 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 og 110, hvoraf summen er 284; og de egentlige divisorer af 284 er 1, 2, 4, 71 og 142, hvoraf summen er 220).
Musikteori
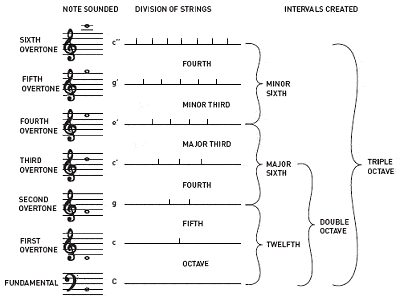
Pythagoras er krediteret for opdagelsen af forholdet mellem harmoniske musikalske toner
Pythagoras er også krediteret for opdagelsen af, at intervallerne mellem harmoniske musikalske toner altid har hele talforhold. For eksempel giver det at spille på en halv længde af en guitarstreng den samme tone som den åbne streng, men en oktav højere; en tredjedel af en længde giver en anden, men harmonisk tone; osv.
Derimod er der en tendens til at give dissonante lyde, hvis man ikke spiller på hele talforhold. På denne måde beskrev Pythagoras de første fire overtoner, som skaber de fælles intervaller, der er blevet de primære byggesten i musikalsk harmoni: oktaven (1:1), den perfekte kvint (3:2), den perfekte kvint (4:3) og den store terts (5:4). Den ældste måde at stemme den 12-toners kromatiske skala på er kendt som pythagoræisk stemning, og den er baseret på en stak perfekte kvintetoner, der hver især er stemt i forholdet 3:2.
Den mystiske Pythagoras var så begejstret for denne opdagelse, at han blev overbevist om, at hele universet var baseret på tal, og at planeterne og stjernerne bevægede sig efter matematiske ligninger, der svarede til musikalske toner, og dermed skabte han en slags symfoni, “Musical Universalis” eller “Sfærernes musik”.
| << Tilbage til græsk matematik | Forward to Plato >> |
