I dette afsnit vil vi gøre os bekendt med mængdelære og notationer, så vi kan anvende disse begreber på både tælle- og sandsynlighedsproblemer. Vi begynder med at definere nogle begreber.
En mængde er en samling af objekter, og dens medlemmer kaldes mængdens elementer. Vi navngiver mængden ved at bruge store bogstaver og omslutter dens medlemmer i krøllede parenteser. Antag, at vi har brug for at opregne medlemmerne af skakklubben. Vi bruger følgende mængdenotation.
C ={Ken, Bob, Tran, Shanti, Eric}
En mængde, der ikke har nogen medlemmer, kaldes en tom mængde. Den tomme mængde betegnes med symbolet Ø.
To mængder er lige store, hvis de har de samme elementer.
En mængde A er en delmængde af en mængde B, hvis ethvert medlem af A også er medlem af B.
Sæt, at C = {Al, Bob, Chris, David, Ed} og A = {Bob, David}. Så er A en delmængde af C, skrevet som 
.
Alle mængder er en delmængde af sig selv, og den tomme mængde er en delmængde af alle mængder.
Union Of Two Sets
Lad A og B være to mængder, så er unionen af A og B, skrevet som 
, mængden af alle elementer, der enten er i A eller i B, eller i både A og B.
Intersektion af to mængder
Lad A og B være to mængder, så er intersektionen af A og B, skrevet som 
, mængden af alle elementer, der er fælles for både mængderne A og B.
En universel mængde U er den mængde, der består af alle elementer, der er under overvejelse.
Komplement til en mængde
Lad A være en hvilken som helst mængde, så er komplementet til mængden A, skrevet som 
, den mængde, der består af de elementer i den universelle mængde U, som ikke er i A.
Disjunkte mængder
To mængder A og B kaldes disjunkte mængder, hvis deres skæringspunkt er en tom mængde.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {orange, grøn, indigo, violet}For at opnå en bedre forståelse, lad os antage, at den universelle mængde U repræsenterer spektrets farver, og P de primære farver, så repræsenterer de farver i spektret, der ikke er primære farver.
.
= {rød, gul, blå, grøn}
= {orange, indigo, violet}
= {rød, gul, blå, violet} = {violet}Venn-diagrammer
Vi bruger nu Venn-diagrammer til at illustrere sammenhængene mellem mængder. I slutningen af 1800-tallet udviklede en engelsk logiker ved navn John Venn en metode til at repræsentere forholdet mellem mængder. Han repræsenterede disse relationer ved hjælp af diagrammer, som nu er kendt som Venn-diagrammer. Et Venn-diagram repræsenterer en mængde som det indre af en cirkel. Ofte er to eller flere cirkler omsluttet af et rektangel, hvor rektanglet repræsenterer den universelle mængde. Det er let at visualisere et skæringspunkt eller en union af en mængde. I dette afsnit vil vi primært bruge Venn-diagrammer til at sortere forskellige populationer og tælle objekter.
|
(a) |
(b) |
(c) |
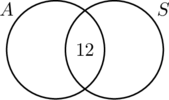
Da 30 personer kørte i biler med automatgear, må cirklen A indeholde 30 elementer. Det betyder, at x + 12 = 30, eller x = 18. På samme måde, da 20 personer kørte i biler med standardgearkasse, må cirkel B indeholde 20 elementer, eller y + 12 = 20, hvilket igen giver y = 8.
Nu, hvor alle oplysningerne er sorteret, er det let at aflæse af diagrammet, at 18 personer kun kørte i biler med automatgear, 12 personer kørte i begge typer biler, og 8 personer kørte kun i biler med standardgearkasse. Derfor deltog 18 + 12 + 8 = 38 personer i undersøgelsen.
|
(a) |
(b) |
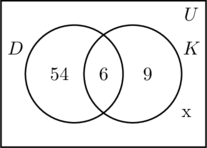
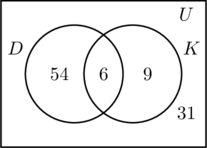
Vi udfylder de tre regioner, der er knyttet til mængderne D og K, på samme måde som før. Da 100 personer deltog i undersøgelsen, må det rektangel, der repræsenterer den universelle mængde U, indeholde 100 objekter. Lad x repræsentere de personer i den universelle mængde, der hverken er i mængden D eller K. Det betyder 54 + 6 + 9 + x = 100, eller x = 31.
Der er derfor 31 personer i undersøgelsen, der hverken har besøgt noget af de to steder.
- 50 jogger, 30 svømmer og 35 cykler
- 14 jogger og svømmer
- 7 svømmer og cykler
- 9 jogger og cykler
- 3 personer deltager i alle tre aktiviteter
Løsning
|
(a) |
(b) |
(c) |
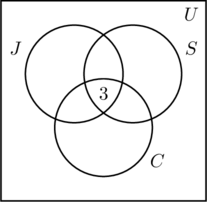
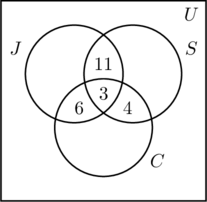
Vi placerer et 3-tal i det inderste område i figur (a), fordi det repræsenterer antallet af personer, der deltager i alle tre aktiviteter. Dernæst beregner vi x, y og z.
- Da 14 personer jogger og svømmer, er x +3 = 14, eller x = 11.
- Da 9 personer jogger og cykler, fås y + 3 = 9, eller y = 6.
- Da 7 personer svømmer og cykler, er z + 3 = 7, eller z = 4.
- Denne information er afbildet i figur (b).
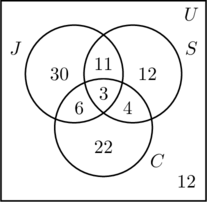
- Da 50 personer jogger, er m + 11 + 6 + 3 + 3 = 50, eller m = 30.
- 30 personer svømmer, derfor er n + 11 + 4 + 3 = 30, eller n = 12.
- 35 personer cykler, derfor er p + 6 + 4 + 3 = 35, eller p = 22.
- Gennem at lægge alle posterne i alle tre sæt sammen, får vi en sum på 88. Da der blev spurgt 100 personer, er antallet inden for det universelle sæt, men uden for alle tre sæt 100 – 88, eller 12.
- I figur (c) er oplysningerne sorteret, og spørgsmålene kan let besvares.
Praksispørgsmål
1. Lad den universelle mængde U = {a, b, c, d, d, e, f, g, h, i, j},V = {a, e, i, f, h}, og W = {a, c, e, g, i}. Angiv medlemmerne af følgende mængder:
a. 
b. 
2. Overvej følgende mængder: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, influenza, Norovirus}, B = {Listeria, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella}, og C = {SARS, Listeria, Tuberkulose, H5N1, Salmonella, HIV, COVID-19}. Angiv medlemmerne af følgende sæt:
a. 
b. 
3. En undersøgelse blandt idrætsudøvere viste, at 30 brugte aspirin mod deres mindre smerter, 50 brugte ibuprofen og 15 brugte begge dele. Alle adspurgte atleter brugte mindst ét af de to smertestillende midler. Hvor mange atleter blev undersøgt?
4. En undersøgelse af 150 gymnasieelever viste, at 25 rapporterede, at de havde haft en tidligere hjernerystelse eller hovedskade, 52 rapporterede, at de havde oplevet psykisk sygdom, og 15 rapporterede begge resultater. Hvor mange elever rapporterede ikke nogen af disse resultater?
5. En undersøgelse blandt 100 studerende på Ryerson University viser, at 50 abonnerer på Netflix, 40 abonnerer på Amazon Prime og 30 abonnerer på Disney+. Af disse abonnerer 15 på både Netflix og Amazon Prime, 10 på både Amazon Prime og Disney+, 10 på både Netflix og Disney+, og 5 har alle tre abonnementstjenester. Tegn et Venn-diagram og bestem følgende:
a. Antallet af studerende, der abonnerer på Amazon Prime, men ikke på de to andre streamingtjenester.
b. Antallet af studerende, der abonnerer på Netflix eller Amazon Prime, men ikke på Disney+.
c. Antallet af studerende, der ikke abonnerer på nogen af disse tjenester.