også kendt som interbedømmertilid eller konkordans
I statistik er interbedømmertilid, interbedømmeroverensstemmelse eller konkordans graden af overensstemmelse mellem bedømmere. Den giver en score på, hvor stor homogenitet eller konsensus der er i de vurderinger, som bedømmerne giver.
De Kappa’er, der er omfattet her, er mest hensigtsmæssige for “nominelle” data. Den naturlige orden i dataene (hvis der findes en sådan) ignoreres af disse metoder. Hvis du vil bruge disse målinger, skal du sørge for at være opmærksom på deres begrænsninger.
Der er to dele til dette:
- Beregne observeret overensstemmelse
- Beregne tilfældig overensstemmelse
Lad os sige, at vi har at gøre med “ja”- og “nej”-svar og to bedømmere. Her er vurderingerne:
rater1 =
rater2 =
Ved omdannelse af disse vurderinger til en forvirringsmatrix:

Observed agreement = (6 + 1) / 10 = 0.7
Chance agreement = probability of randomly saying yes (P_yes) + probability of randomly saying no (P_no)
P_yes = (6 + 1) / 10 * (6 + 1) / 10 = 0.49
P_no = (1 + 1) / 10 * (1 + 1) / 10 = 0.04
Chance agreement = 0.49 + 0.04 = 0.53
Da den observerede overensstemmelse er større end tilfældighedens overensstemmelse, får vi en positiv Kappa.
kappa = 1 - (1 - 0.7) / (1 - 0.53) = 0.36
Og du kan bare bruge sklearns implementering
from sklearn.metrics import cohen_kappa_scorecohen_kappa_score(rater1, rater2)
som returnerer 0,35714.
Interpretation af Kappa

Speciale tilfælde
Mindre end tilfældig overensstemmelse
rater1 =
rater2 =
cohen_kappa_score(rater1, rater2)
-0.2121
Hvis alle vurderingerne er ens og modsat
Dette tilfælde giver pålideligt en kappa på 0
rater1 = * 10
rater2 = * 10
cohen_kappa_score(rater1, rater2)
0.0
Randomvurderinger
For tilfældige vurderinger følger Kappa en normalfordeling med en middelværdi på omkring nul.
Da antallet af bedømmelser stiger, er der mindre variabilitet i værdien af Kappa i fordelingen.
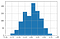
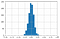
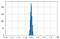
Du kan finde flere detaljer her
Bemærk, at Cohen’s Kappa kun gælder for 2 bedømmere, der bedømmer nøjagtig de samme emner.
