En gruppe 
er et endeligt eller uendeligt sæt af elementer sammen med en binær operation (kaldet gruppeoperationen), der tilsammen opfylder de fire grundlæggende egenskaber lukkethed, associativitet, identitetsegenskaben og den omvendte egenskab. Den operation, i forhold til hvilken en gruppe er defineret, kaldes ofte “gruppeoperation”, og en mængde siges at være en gruppe “under” denne operation. Elementer 
, 
, 
, … med binær operation mellem 
og 
betegnet 
danner en gruppe, hvis
1. Lukning: Hvis 
og 
er to elementer i 
, så er produktet 
også i 
.
2. Associativitet: Den definerede multiplikation er associativ, dvs. for alle 
, 
.
3. Identitet: Der findes et identitetselement 
(også kaldet 1, 
eller 
), således at 
for hvert element 
.
4. Omvendt: Der skal være en omvendt (også kaldet reciprok) af hvert element. Derfor indeholder mængden for hvert element 
af 
et element 
, således at 
.
En gruppe er en monoide, hvis elementer hver især er invertible.
En gruppe skal indeholde mindst ét element, idet den unikke (op til isomorfi) enkeltelementgruppe er kendt som den trivielle gruppe.
Læren om grupper kaldes gruppeteori. Hvis der er et endeligt antal elementer, kaldes gruppen en endelig gruppe, og antallet af elementer kaldes gruppens gruppeorden. En delmængde af en gruppe, der er lukket under gruppeoperationen og den omvendte operation, kaldes en undergruppe. Undergrupper er også grupper, og mange almindeligt forekommende grupper er i virkeligheden specielle undergrupper af en eller anden mere generel større gruppe.
Et grundlæggende eksempel på en endelig gruppe er den symmetriske gruppe 
, som er gruppen af permutationer (eller “under permutation”) af 
objekter. Den enkleste uendelige gruppe er mængden af hele tal under sædvanlig addition. For kontinuerte grupper kan man overveje de reelle tal eller mængden af 
invertible matricer. De to sidste er eksempler på Lie-grupper.
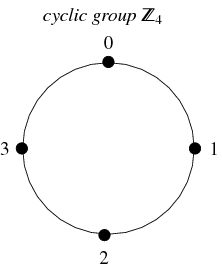
En meget almindelig gruppetype er de cykliske grupper. Denne gruppe er isomorf til gruppen af hele tal (modulo 
), betegnes 
, 
eller 
, og er defineret for hvert heltal 
. Den er lukket under addition, er associativ og har unikke inverser. Tallene fra 0 til 
repræsenterer dens elementer, idet identitetselementet er repræsenteret ved 0, og inversen af 
er repræsenteret ved 
.
Et kort mellem to grupper, der bevarer identiteten og gruppeoperationen, kaldes en homomorfi. Hvis en homomorfisme har en omvendt, som også er en homomorfisme, kaldes den en isomorfisme, og de to grupper kaldes isomorfe. To grupper, der er isomorfe for hinanden, anses for at være “de samme”, når de betragtes som abstrakte grupper. For eksempel er gruppen af rotationer af et kvadrat, illustreret nedenfor, den cykliske gruppe 
.
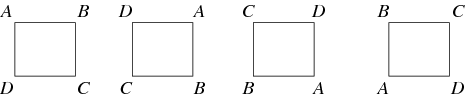
Generelt er der tale om en gruppeaktion, når en gruppe virker på en mængde ved at permutere dens elementer, således at kortet fra gruppen til mængdens permutationsgruppe er en homomorfi. F.eks. er rotationerne af et kvadrat en undergruppe af permutationerne af dets hjørner. En vigtig gruppehandling for enhver gruppe 
er dens handling på sig selv ved konjugation. Dette er blot nogle af de mulige gruppeautomorphismer. En anden vigtig form for gruppeaktion er en grupperepræsentation, hvor gruppen virker på et vektorrum ved hjælp af inverterbare lineære kort. Når vektorrummets felt er de komplekse tal, kaldes en repræsentation undertiden et CG-modul.
Gruppehandlinger, og især repræsentationer, er meget vigtige i anvendelser, ikke kun inden for gruppeteori, men også inden for fysik og kemi. Da en gruppe kan opfattes som et abstrakt matematisk objekt, kan den samme gruppe optræde i forskellige sammenhænge. Det er derfor nyttigt at tænke på en repræsentation af gruppen som en bestemt inkarnation af gruppen, som også kan have andre repræsentationer. En irreducible repræsentation af en gruppe er en repræsentation, for hvilken der ikke findes nogen enhedstransformation, som vil omdanne repræsentationsmatrixen til blokdiagonal form. De irreducible repræsentationer har en række bemærkelsesværdige egenskaber, som er formaliseret i gruppens ortogonalitetsteorem.