Læringsmål
I slutningen af dette afsnit vil du være i stand til:
- Beskriv et typisk fotoelektrisk eksperiment.
- Bestemme den maksimale kinetiske energi af fotoelektroner, der udsendes af fotoner med én energi eller bølgelængde, når man får den maksimale kinetiske energi af fotoelektroner for en anden fotonenergi eller bølgelængde.
Når lys rammer materialer, kan det udsende elektroner fra dem. Dette kaldes den fotoelektriske effekt, hvilket betyder, at lys (foto) producerer elektricitet. En almindelig anvendelse af den fotoelektriske effekt er i lysmålere, som f.eks. dem, der justerer den automatiske blænde på forskellige typer kameraer. På samme måde anvendes det også i solceller, som du sikkert har i din lommeregner eller har set på et tag eller et vejskilt. Disse gør brug af den fotoelektriske effekt til at omdanne lys til elektricitet til at drive forskellige apparater.

Figur 1. Den fotoelektriske effekt kan iagttages ved at lade lys falde på metalpladen i dette evakuerede rør. Elektroner, der kastes ud af lyset, opsamles på samlertråden og måles som en strøm. En forsinkelsesspænding mellem samlertråden og pladen kan derefter justeres for at bestemme energien af de udskudte elektroner. Hvis den f.eks. er tilstrækkelig negativ, vil ingen elektroner nå frem til ledningen. (credit: P.P. Urone)
Denne effekt har været kendt i mere end et århundrede og kan studeres ved hjælp af en anordning som den, der er vist i figur 1. Denne figur viser et evakueret rør med en metalplade og en kollektortråd, der er forbundet med en variabel spændingskilde, hvor kollektoren er mere negativ end pladen. Når lys (eller anden EM-stråling) rammer pladen i det evakuerede rør, kan den udstøde elektroner. Hvis elektronerne har en energi i elektronvolt (eV), der er større end potentialforskellen mellem pladen og ledningen i volt, vil nogle af elektronerne blive opsamlet på ledningen. Da elektronenergien i eV er eV, hvor q er elektronladningen og V er potentialforskellen, kan elektronenergien måles ved at justere den forsinkende spænding mellem ledningen og pladen. Den spænding, der forhindrer elektronerne i at nå frem til ledningen, er lig med energien i eV. Hvis f.eks. -3,00 V knap nok stopper elektronerne, er deres energi 3,00 eV. Antallet af udskudte elektroner kan bestemmes ved at måle strømmen mellem ledningen og pladen. Jo mere lys, jo flere elektroner; et lille kredsløb gør det muligt at bruge denne anordning som lysmåler.
Det virkelig vigtige ved den fotoelektriske effekt er det, som Albert Einstein udledte af den. Einstein indså, at der var flere karakteristika ved den fotoelektriske effekt, som kun kunne forklares, hvis EM-stråling i sig selv er kvantiseret: Den tilsyneladende kontinuerlige strøm af energi i en EM-bølge består i virkeligheden af energikvanter kaldet fotoner. I sin forklaring af den fotoelektriske effekt definerede Einstein en kvantiseret enhed eller kvante af EM-energi, som vi nu kalder en foton, med en energi, der er proportional med EM-strålingens frekvens. I ligningsform er fotonenergien E = hf, hvor E er energien af en foton med frekvensen f, og h er Plancks konstant. Denne revolutionerende idé ligner Plancks kvantisering af energitilstande i sortkropsoscillatorer, men den er helt anderledes. Det er selve kvantiseringen af EM-stråling. EM-bølger består af fotoner og er ikke kontinuerlige glatte bølger, som beskrevet i tidligere kapitler om optik. Deres energi absorberes og udsendes i klumper, ikke kontinuerligt. Dette er nøjagtigt i overensstemmelse med Plancks kvantisering af energiniveauer i sortkropsoscillatorer, da disse oscillatorer øger og reducerer deres energi i trin på hf ved at absorbere og udsende fotoner, der har E = hf. Vi observerer ikke dette med vores øjne, fordi der er så mange fotoner i almindelige lyskilder, at de enkelte fotoner går ubemærket hen. (Se figur 2.) Det næste afsnit af teksten (Photon-energier og det elektromagnetiske spektrum) er afsat til en diskussion af fotoner og nogle af deres egenskaber og konsekvenser. Indtil videre vil vi bruge fotonbegrebet til at forklare den fotoelektriske effekt, ganske som Einstein gjorde.
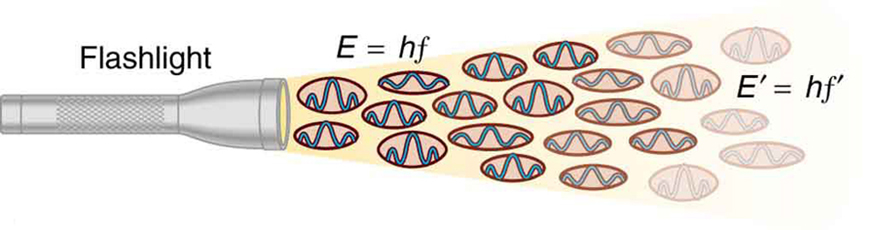
Figur 2. En EM-bølge med frekvensen f er sammensat af fotoner eller individuelle kvanta af EM-stråling. Energien af hver foton er E = hf, hvor h er Plancks konstant, og f er frekvensen af EM-strålingen. Højere intensitet betyder flere fotoner pr. arealenhed. Lommelygten udsender et stort antal fotoner med mange forskellige frekvenser, og derfor har andre fotoner energi E′ = hf′ osv.
Den fotoelektriske effekt har de egenskaber, der diskuteres nedenfor. Alle disse egenskaber er i overensstemmelse med tanken om, at individuelle fotoner af EM-stråling absorberes af individuelle elektroner i et materiale, hvorved elektronen opnår fotonens energi. Nogle af disse egenskaber er uforenelige med ideen om, at EM-stråling er en simpel bølge. Lad os for enkelhedens skyld se på, hvad der sker med monokromatisk EM-stråling, hvor alle fotoner har den samme energi hf.
- Hvis vi varierer frekvensen af den EM-stråling, der falder på et materiale, finder vi følgende: For et givet materiale er der en tærskelfrekvens f0 for EM-strålingen, under hvilken ingen elektroner bliver kastet ud, uanset intensiteten. De enkelte fotoner vekselvirker med de enkelte elektroner. Hvis fotonenergien er for lille til at bryde en elektron væk, vil ingen elektroner blive skudt ud. Hvis EM-strålingen var en simpel bølge, kunne der opnås tilstrækkelig energi ved at øge intensiteten.
- Når EM-strålingen falder på et materiale, bliver elektronerne uden forsinkelse skudt ud. Så snart en individuel foton med en tilstrækkelig høj frekvens absorberes af en individuel elektron, bliver elektronen udstødt. Hvis EM-strålingen var en simpel bølge, ville det tage adskillige minutter, før tilstrækkelig energi er deponeret på metaloverfladen til at udstøde en elektron.
- Antal af udstødte elektroner pr. tidsenhed er proportionalt med EM-strålingens intensitet og ikke med nogen anden egenskab. EM-stråling med høj intensitet består af et stort antal fotoner pr. arealenhed, hvor alle fotoner har den samme karakteristiske energi hf.
- Hvis vi varierer EM-strålingens intensitet og måler energien af de udskudte elektroner, finder vi følgende: Den maksimale kinetiske energi af de udskudte elektroner er uafhængig af intensiteten af EM-strålingen. Da der er så mange elektroner i et materiale, er det yderst usandsynligt, at to fotoner vil vekselvirke med den samme elektron på samme tid og derved øge den givne energi. I stedet (som nævnt i punkt 3 ovenfor) resulterer en øget intensitet i, at flere elektroner med den samme energi bliver udsendt. Hvis EM-stråling var en simpel bølge, kunne en højere intensitet give mere energi, og elektroner med højere energi ville blive skudt ud.
- Den kinetiske energi af en udskudt elektron er lig med fotonenergien minus elektronens bindingsenergi i det specifikke materiale. En enkelt foton kan afgive hele sin energi til en elektron. Fotonens energi bruges delvist til at bryde elektronen væk fra materialet. Den resterende del går til den udskudte elektrons kinetiske energi. I ligningsform er dette givet ved KEe = hf – BE, hvor KEe er den maksimale kinetiske energi af den udskudte elektron, hf er fotonens energi, og BE er elektronens bindingsenergi til det pågældende materiale. (BE kaldes undertiden materialets arbejdsfunktion.) Denne ligning, der stammer fra Einstein i 1905, forklarer egenskaberne ved den fotoelektriske effekt kvantitativt. En individuel foton af EM-stråling (den kommer ikke på anden måde) vekselvirker med en individuel elektron og tilfører nok energi, BE, til at bryde den fra hinanden, mens resten går til kinetisk energi. Bindingsenergien er BE = hf0, hvor f0 er tærskelfrekvensen for det pågældende materiale. Figur 3 viser en graf over den maksimale KEe over for frekvensen af den indfaldende EM-stråling, der falder på et bestemt materiale.
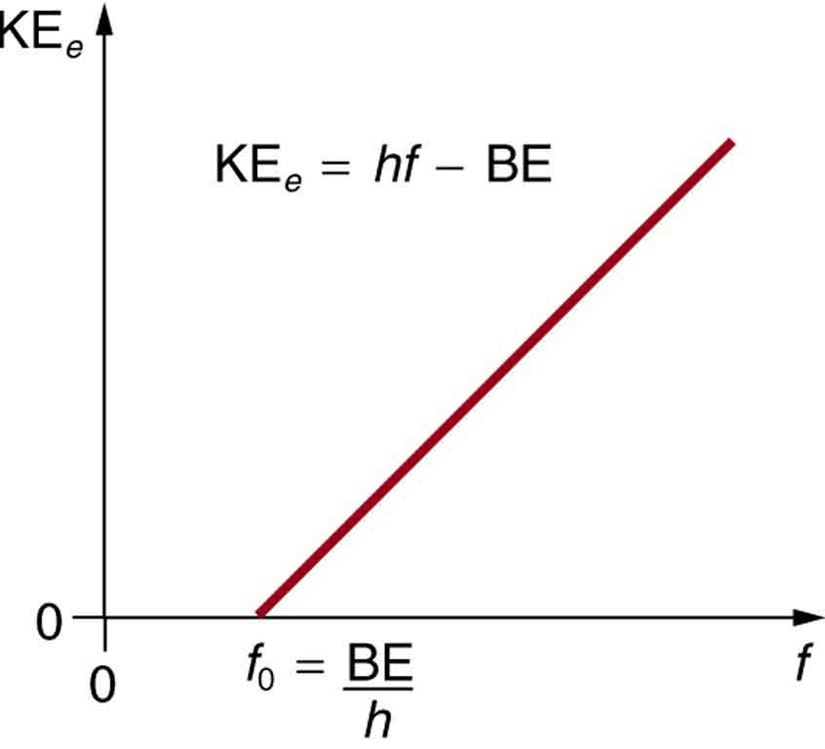
Figur 3. Fotoelektrisk effekt. Graf over den kinetiske energi af en udskudt elektron, KEe, mod frekvensen af den EM-stråling, der falder på et bestemt materiale. Der er en tærskelfrekvens, under hvilken ingen elektroner kastes ud, fordi den enkelte foton, der interagerer med en enkelt elektron, ikke har tilstrækkelig energi til at bryde den væk. Over tærskelenergien stiger KEe lineært med f, hvilket er i overensstemmelse med KEe = hf – BE. Hældningen af denne linje er h – dataene kan bruges til at bestemme Plancks konstant eksperimentelt. Einstein gav den første vellykkede forklaring på sådanne data ved at foreslå ideen om fotoner – kvanta af EM-stråling.
Einsteins idé om, at EM-stråling er kvantiseret, var afgørende for kvantemekanikkens begyndelse. Det er et langt mere generelt begreb, end dets forklaring af den fotoelektriske effekt kunne antyde. Al EM-stråling kan også modelleres i form af fotoner, og EM-strålingens karakteristika er helt i overensstemmelse med dette faktum. (Som vi vil se i næste afsnit, kan mange aspekter af EM-stråling, som f.eks. farerne ved ultraviolet (UV) stråling, kun forklares ved hjælp af fotonernes egenskaber). Einstein, der er mere berømt for den moderne relativitetsteori, plantede et vigtigt frø til kvantemekanikken i 1905, samme år som han udgav sin første artikel om den specielle relativitetsteori. Hans forklaring af den fotoelektriske effekt var grundlaget for Nobelprisen, som han fik tildelt i 1921. Selv om hans andre bidrag til den teoretiske fysik også blev nævnt i denne pris, blev den specielle og generelle relativitetsteori ikke fuldt ud anerkendt på trods af, at den delvist var blevet verificeret ved eksperiment i 1921. Selv om denne store mand blev tilbedt som en helt, fik han aldrig nobelpris for sit mest berømte værk, relativitetsteorien.
Eksempel 1. Beregning af fotonenergi og den fotoelektriske effekt: Et violet lys
1. Hvad er energien i joule og elektronvolt for en foton af 420 nm violet lys?
2. Hvad er den maksimale kinetiske energi af de elektroner, der kastes ud af calcium ved 420 nm violet lys, givet at elektronernes bindingsenergi (eller arbejdsfunktion) for calciummetal er 2,71 eV?
Strategi
For at løse del 1 skal du bemærke, at en fotons energi er givet ved E = hf. Til del 2 er det, når fotonens energi er beregnet, en simpel anvendelse af KEe = hf – BE for at finde den udskudte elektrons maksimale kinetiske energi, da BE er givet.
Løsning af del 1
Photonenergien er givet ved E = hf.
Da vi får bølgelængden i stedet for frekvensen, løser vi den velkendte relation c = fλ for frekvensen, hvilket giver f=\frac{c}{\lambda}\\\.
Kombination af disse to ligninger giver den nyttige relation E=\frac{hc}{\lambda}\\.
Nu giver substitution af kendte værdier
\displaystyle{E}=\frac{\left(6.63\times10^{-34}\text{ J}\cdot\text{ s}\right)\left(3.00\times10^{8}\text{ m/s}\right)}{420\times10^{-9}\text{ m}}}=4.74\times10^{-19}\text{ J}\\\
Omregnet til eV er fotonens energi
\displaystyle{E}=\left(4.47\times10^{-19}\text{ J}\right)\frac{1\text{ eV}}}{1.6\times10^{-19}\text{ J}}}=2.96\text{ eV}\\\
Løsning til del 2
Findelse af den kinetiske energi af den udskudte elektron er nu en simpel anvendelse af ligningen KEe = hf – BE. Ved at erstatte fotonenergien og bindingsenergien fås KEe = hf – BE = 2,96 eV – 2,71 eV = 0,246 eV.
Diskussion
Energien af denne 420 nm foton af violet lys er en lille brøkdel af en joule, og det er derfor ikke underligt, at en enkelt foton ville være vanskelig for os at opfatte direkte – mennesker er mere indstillet på energier i størrelsesordenen joule. Men hvis vi ser på energien i elektronvolt, kan vi se, at denne foton har energi nok til at påvirke atomer og molekyler. Et DNA-molekyle kan f.eks. brydes med ca. 1 eV energi, og typiske atom- og molekylære energier er i størrelsesordenen eV, så UV-fotonerne i dette eksempel kan have biologiske virkninger. Den udskudte elektron (kaldet en fotoelektron) har en ret lav energi, og den vil ikke kunne bevæge sig langt, undtagen i et vakuum. Elektronen ville blive stoppet af et forsinkelsespotentiale på kun 0,26 eV. Hvis fotonens bølgelængde var længere og dens energi mindre end 2,71 eV, ville formlen give en negativ kinetisk energi, hvilket er en umulighed. Det betyder ganske enkelt, at 420-nm-fotonerne med deres energi på 2,96 eV ikke er meget over frekvensgrænsen. Du kan selv vise, at tærskelbølgelængden er 459 nm (blåt lys). Det betyder, at hvis der anvendes calciummetal i en lysmåler, vil måleren være ufølsom over for bølgelængder, der er længere end bølgelængderne for blåt lys. En sådan lysmåler ville f.eks. være helt ufølsom over for rødt lys.
PhET Explorations: Fotoelektrisk effekt
Se, hvordan lys slår elektroner ud af et metalmål, og genskab det eksperiment, som gav anledning til kvantemekanikken.

Klik for at downloade simuleringen. Kør ved hjælp af Java.
Sammenfatning af afsnittet
- Den fotoelektriske effekt er den proces, hvor EM-stråling skubber elektroner ud af et materiale.
- Einstein foreslog, at fotoner er kvanta af EM-stråling med energien E = hf, hvor f er strålingens frekvens.
- Al EM-stråling består af fotoner. Som Einstein forklarede, skyldes alle karakteristika ved den fotoelektriske effekt vekselvirkningen mellem individuelle fotoner og individuelle elektroner.
- Den maksimale kinetiske energi KEe for udskudte elektroner (fotoelektroner) er givet ved KEe = hf – BE, hvor hf er fotonenergien og BE er elektronens bindingsenergi (eller arbejdsfunktion) til det pågældende materiale.
Begrebsspørgsmål
- Er synligt lys den eneste type EM-stråling, der kan forårsage den fotoelektriske effekt?
- Hvilke aspekter af den fotoelektriske effekt kan ikke forklares uden fotoner? Hvilke kan forklares uden fotoner? Er sidstnævnte uforenelige med eksistensen af fotoner?
- Er den fotoelektriske effekt en direkte konsekvens af EM-strålingens bølgekarakter eller af EM-strålingens partikelkarakter? Forklar kort.
- Insolatorer (ikke-metaller) har en højere BE end metaller, og det er vanskeligere for fotoner at skubbe elektroner ud af isolatorer. Diskuter, hvordan dette hænger sammen med de frie ladninger i metaller, der gør dem til gode ledere.
- Hvis man tager et stykke metal op og ryster det, som har elektroner i sig, der frit kan bevæge sig som en strøm, falder der ingen elektroner ud. Men hvis man opvarmer metallet, kan elektroner koges ud. Forklar begge disse forhold i forhold til mængden og fordelingen af energi ved at ryste genstanden sammenlignet med opvarmning af den.
Opgaver & Opgaver
- Hvad er den længste bølgelængde af EM-stråling, der kan udstøde en fotoelektron fra sølv, hvis bindingsenergien er 4,73 eV? Er dette i det synlige område?
- Find den foton med den længste bølgelængde, der kan udstøde en elektron fra kalium, idet bindingsenergien er 2,24 eV. Er dette synlig EM-stråling?
- Hvad er bindingsenergien i eV for elektroner i magnesium, hvis den længste foton, der kan udstøde elektroner, er 337 nm?
- Beregne bindingsenergien i eV for elektroner i aluminium, hvis den længste foton, der kan udstøde dem, er 304 nm.
- Hvad er den maksimale kinetiske energi i eV for de elektroner, der skubbes ud af natriummetal ved EM-stråling på 450 nm, givet at bindingsenergien er 2,28 eV?
- UV-stråling med en bølgelængde på 120 nm falder på guldmetal, hvortil elektronerne er bundet med 4,82 eV. Hvad er den maksimale kinetiske energi for de udskudte fotoelektroner?
- Violet lys med en bølgelængde på 400 nm udstøder elektroner med en maksimal kinetisk energi på 0,860 eV fra natriummetal. Hvad er elektronernes bindingsenergi til natriummetal?
- UV-stråling med en bølgelængde på 300 nm falder på uranmetal og udstøder elektroner med en bølgelængde på 0,500 eV. Hvad er elektronernes bindingsenergi til uranmetal?
- (a) Hvad er bølgelængden af den EM-stråling, der udstøder 2,00 eV elektroner fra calciummetal, givet at bindingsenergien er 2,71 eV? (b) Hvilken type EM-stråling er dette?
- Find bølgelængden af fotoner, der udstøder 0,100-eV-elektroner fra kalium, givet at bindingsenergien er 2,24 eV. Er disse fotoner synlige?
- Hvad er den maksimale hastighed for de elektroner, der skubbes ud fra et materiale af 80 nm fotoner, hvis de er bundet til materialet med 4,73 eV?
- Fotoelektroner fra et materiale med en bindingsenergi på 2,71 eV skubbes ud af 420 nm fotoner. Hvor lang tid tager det disse elektroner, når de er kastet ud, at bevæge sig 2,50 cm til en detektionsanordning?
- En laser med en udgangseffekt på 2,00 mW ved en bølgelængde på 400 nm projiceres på calciummetal. (a) Hvor mange elektroner pr. sekund kastes ud? (b) Hvilken effekt transporteres væk af elektronerne, idet bindingsenergien er 2,71 eV?
- (a) Beregn antallet af fotoelektroner pr. sekund, der udstødes fra et område på 1,00 mm 2 af natriummetal ved EM-stråling på 500 nm med en intensitet på 1,30 kW/m2 (intensiteten af sollys over jordens atmosfære). (b) I betragtning af at bindingsenergien er 2,28 eV, hvilken effekt transporteres væk af elektronerne? (c) Elektronerne transporterer mindre energi væk end den, som fotonerne bringer med sig. Hvor går den anden energi hen? Hvordan kan den genvindes?
- Ufornuftige resultater. Rødt lys med en bølgelængde på 700 nm projiceres på magnesiummetal, som elektronerne er bundet til med 3,68 eV. (a) Brug KEe = hf – BE til at beregne den kinetiske energi af de udskudte elektroner. (b) Hvad er urimeligt ved dette resultat? (c) Hvilke antagelser er urimelige eller inkonsekvente?
- Urimelige resultater. (a) Hvad er elektronernes bindingsenergi til et materiale, hvorfra 4,00-eV-elektroner kastes ud ved 400 nm EM-stråling? (b) Hvad er urimeligt ved dette resultat? (c) Hvilke forudsætninger er urimelige eller inkonsekvente?
Glossar
fotoelektrisk effekt: det fænomen, hvorved nogle materialer udstøder elektroner, når lys skinner på dem
foton: et kvantum, eller en partikel, af elektromagnetisk stråling
foton-energi: den energimængde, som en foton har; E = hf
Bindingsenergi: også kaldet arbejdsfunktionen; den energimængde, der er nødvendig for at udstøde en elektron fra et materiale
Udvalgte løsninger på problemer & Opgaver
1. 263 nm
3. 3,69 eV
5. 0,483 eV
7. 2,25 eV
9. (a) 264 nm; (b) ultraviolet
11. 1,95 × 106 m/s
13. (a) 4,02 × 1015 s; (b) 0,256 mW
15. (a) -1,90 eV; (b) Negativ kinetisk energi; (c) At elektronerne ville blive slået fri.
