Vandets fasediagram
Figur 11.23 “To versioner af vandets fasediagram” viser vandets fasediagram og illustrerer, at vandets trippelpunkt forekommer ved 0,01 °C og 0,00604 atm (4,59 mmHg). Tripelpunktet (273,16 K) er langt mere reproducerbart end isens smeltepunkt, som afhænger af mængden af opløst luft og det atmosfæriske tryk, og det bruges til at definere den absolutte temperaturskala (Kelvin). Tripelpunktet repræsenterer også det laveste tryk, ved hvilket en flydende fase kan eksistere i ligevægt med fast stof eller damp. Ved tryk under 0,00604 atm smelter is derfor ikke til en væske, når temperaturen stiger; det faste stof sublimerer direkte til vanddamp. Sublimation af vand ved lav temperatur og lavt tryk kan bruges til at “frysetørre” fødevarer og drikkevarer. Fødevarerne eller drikkevarerne afkøles først til temperaturer under nul og anbringes i en beholder, hvor trykket holdes under 0,00604 atm. Efterhånden som temperaturen øges, sublimerer vandet og efterlader den dehydrerede mad (som den, der bruges af rygsækrejsende eller astronauter) eller den pulveriserede drik (som med frysetørret kaffe).
Fasediagrammet for vand illustreret i del (b) i figur 11.23 “Two Versions of the Phase Diagram of Water” viser grænsen mellem is og vand i en udvidet skala. Isens smeltekurve hælder opad og lidt til venstre i stedet for opad og til højre som i figur 11.22 “Et typisk fasediagram for et stof, der udviser tre faser – fast, flydende og gas – og et superkritisk område”; det vil sige, at isens smeltepunkt falder med stigende tryk; ved 100 MPa (987 atm) smelter isen ved -9 °C. Vand opfører sig på denne måde, fordi det er et af de få kendte stoffer, for hvilke det krystallinske faste stof er mindre tæt end væsken (andre omfatter antimon og bismuth). Hvis trykket på is, der er i ligevægt med vand ved 0 °C og 1 atm, øges, vil nogle af molekylerne blive presset tættere sammen, hvorved prøvens volumen mindskes. Volumenreduktionen (og den tilsvarende forøgelse af densiteten) er mindre for et fast stof eller en væske end for en gas, men den er tilstrækkelig til at smelte noget af isen.
Figur 11.23 To versioner af vands fasediagram
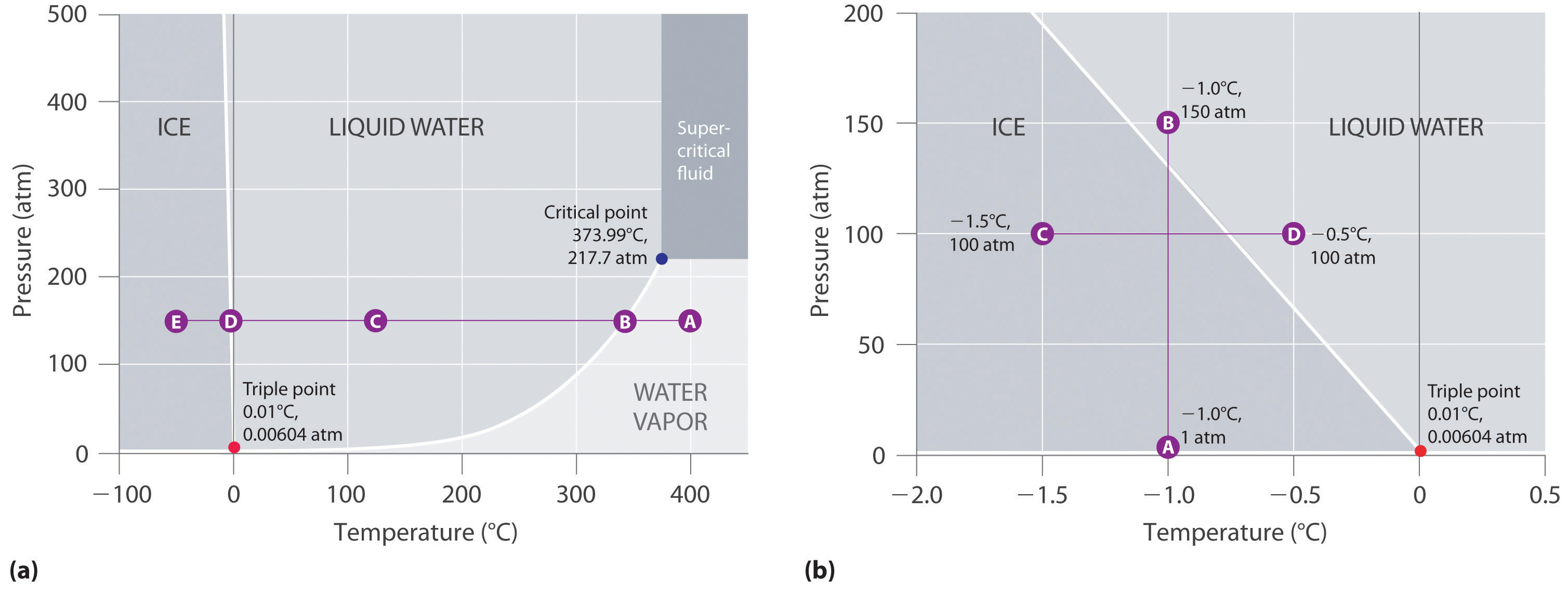
(a) I denne graf med lineære temperatur- og trykakser er grænsen mellem is og flydende vand næsten lodret. (b) Denne graf med en udvidet skala illustrerer faldet i smeltepunktet med stigende tryk. (Bogstaverne henviser til punkter, der er diskuteret i eksempel 10.)
I del (b) i figur 11.23 “To versioner af vands fasediagram” er punkt A placeret ved P = 1 atm og T = -1,0 °C, inden for det faste (is) område af fasediagrammet. Når trykket øges til 150 atm, mens temperaturen forbliver den samme, krydser linjen fra punkt A is/vand-grænsen til punkt B, som ligger i det flydende vandområde. Hvis man anvender et tryk på 150 atm, vil isen derfor smelte ved -1,0 °C. Vi har allerede antydet, at trykafhængigheden af vands smeltepunkt er af afgørende betydning. Hvis grænsen mellem fast/flydende i vands fasediagram skulle skråt opad og til højre i stedet for til venstre, ville is være tættere end vand, isterninger ville synke, vandrør ville ikke sprænge, når de fryser, og frostvæske ville være unødvendig i bilmotorer.
Sindtil for nylig beskrev mange lærebøger skøjteløb som værende muligt, fordi det tryk, der genereres af skøjteløberens klinge, er højt nok til at smelte isen under klingen og derved skabe et smørende lag af flydende vand, der gør det muligt for klingen at glide hen over isen. Selv om denne forklaring er intuitivt tilfredsstillende, er den forkert, som vi kan vise ved en simpel beregning. Husk fra kapitel 10 “Gasser”, at tryk (P) er den kraft (F), der udøves pr. arealenhed (A):
Geligning 11.4
P = F A
For at beregne det tryk, som en skøjteløber udøver på isen, behøver vi kun at beregne den udøvede kraft og arealet af skøjtebladet. Hvis vi antager en skøjteløber på 75,0 kg (165 lb), er den kraft, som skøjteløberen udøver på isen som følge af tyngdekraften,
Betegnelse 11.5
F = mg
hvor m er massen, og g er accelerationen som følge af jordens tyngdekraft (9,81 m/s2). Kraften er således
Glidning 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Hvis vi antager, at skøjtebladene er 2.0 mm brede og 25 cm lange, så er arealet af bunden af hver klinge
Bedømmelse 11.7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Hvis skøjteløberen glider på en fod, er det tryk, der udøves på isen
Sammenligning 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
Trykket er meget lavere end det tryk, der skal til for at sænke isens smeltepunkt med blot 1 °C, og erfaringen viser, at det er muligt at skøjte, selv når temperaturen er et godt stykke under frysepunktet. Trykinduceret smeltning af isen kan således ikke forklare den lave friktion, der gør det muligt for skøjteløbere (og ishockeypucks) at glide. Nyere forskning tyder på, at isens overflade, hvor den ordnede række af vandmolekyler møder luften, består af et eller flere lag af næsten flydende vand. Disse lag synes sammen med den smeltning, der fremkaldes af friktionen, når en skøjteløber skubber sig fremad, at kunne forklare både den lethed, hvormed en skøjteløber glider, og det faktum, at det bliver vanskeligere at skøjte under ca. -7 °C, når antallet af smørende vandlag på overfladen mindskes.
