neboli spolehlivost mezi hodnotiteli nebo konkordance
Ve statistice je spolehlivost mezi hodnotiteli, shoda mezi hodnotiteli nebo konkordance míra shody mezi hodnotiteli. Udává, jaká je míra homogenity neboli shody v hodnoceních udělených posuzovateli.
Kappy, kterými se zde zabýváme, jsou nejvhodnější pro „nominální“ údaje. Přirozené uspořádání v datech (pokud nějaké existuje) tyto metody ignorují. Pokud se chystáte tyto metriky používat, ujistěte se, že jste si vědomi jejich omezení.
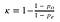
Tady jsou dvě části:
- Vypočítejte pozorovanou shodu
- Vypočítejte shodu náhodně
Řekněme, že máme co do činění s odpověďmi „ano“ a „ne“ a dvěma hodnotiteli. Zde jsou hodnocení:
rater1 =
rater2 =
Převedeme-li tato hodnocení do matice záměny:

Observed agreement = (6 + 1) / 10 = 0.7
Chance agreement = probability of randomly saying yes (P_yes) + probability of randomly saying no (P_no)
P_yes = (6 + 1) / 10 * (6 + 1) / 10 = 0.49
P_no = (1 + 1) / 10 * (1 + 1) / 10 = 0.04
Chance agreement = 0.49 + 0.04 = 0.53
Protože pozorovaná shoda je větší než shoda náhodná, dostaneme kladné Kappa.
kappa = 1 - (1 - 0.7) / (1 - 0.53) = 0.36
Nebo stačí použít implementaci sklearn
from sklearn.metrics import cohen_kappa_scorecohen_kappa_score(rater1, rater2)
která vrátí 0,35714.
Interpretace Kappa

Speciální případy
Méně než náhodná shoda
rater1 =
rater2 =
cohen_kappa_score(rater1, rater2)
-0.2121
Pokud jsou všechny. hodnocení jsou stejná a opačná
Tento případ spolehlivě dává kappa 0
rater1 = * 10
rater2 = * 10
cohen_kappa_score(rater1, rater2)
0.0
Náhodné hodnocení
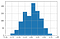
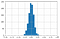
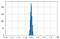
Pro náhodné hodnocení Kappa platí normální rozdělení se střední hodnotou kolem nuly.
S rostoucím počtem hodnocení je v rozdělení menší variabilita hodnoty Kappa.
Podrobnější informace najdete zde
Všimněte si, že Cohenova Kappa platí pouze pro 2 hodnotitele, kteří hodnotí naprosto stejné položky.
