
Pythagoras ze Samu (asi 570-495). př. n. l.)
Biografie – Kdo byl Pythagoras
Někdy se tvrdí, že za čistou matematiku vděčíme Pythagorovi, a často se mu říká první „pravý“ matematik. Ačkoli však byl jeho přínos zjevně významný, přesto zůstává kontroverzní postavou.
Sám nezanechal žádné matematické spisy a většina toho, co víme o pythagorejském myšlení, k nám přichází ze spisů Filoláa a dalších pozdějších pythagorejských učenců. Není totiž vůbec jasné, zda mnohé (nebo dokonce žádné) z jemu připisovaných vět skutečně vyřešil Pythagoras osobně nebo jeho následovníci.
Škola, kterou založil v Krotonu v jižní Itálii kolem roku 530 př. n. l., byla jádrem poněkud bizarní pythagorejské sekty. Ačkoli pythagorejskému myšlení do značné míry dominovala matematika, bylo také hluboce mystické a Pythagoras všem členům své školy vnucoval svou kvazináboženskou filozofii, přísné vegetariánství, společný život, tajné obřady a podivná pravidla (včetně bizarních a zřejmě nahodilých nařízení o tom, že nikdy nemají močit směrem ke slunci, nikdy si nemají brát ženu, která nosí zlaté šperky, nikdy nemají míjet osla ležícího na ulici, nikdy nemají jíst nebo se dokonce dotýkat černých fazolí fava apod.
Členové se dělili na „mathematikoi“ (neboli „žáky“), kteří rozšiřovali a rozvíjeli více matematické a vědecké práce, jež začal sám Pythagoras, a „akousmatikoi“ (neboli „posluchače“), kteří se zaměřovali na více náboženské a rituální aspekty jeho učení. Mezi oběma skupinami vždy existovaly určité třenice a nakonec se sekta zapletla do ostrých místních bojů a nakonec se rozpadla. Proti tajnůstkářství a výlučnosti pythagorejců se zvedla vlna nevole a v roce 460 př. n. l. byla všechna místa jejich setkávání vypálena a zničena, přičemž jen v Krotonu bylo zabito nejméně 50 jejich členů.
Převládajícím diktátem Pythagorovy školy bylo „Vše je číslo“ nebo „Bůh je číslo“ a pythagorejci fakticky praktikovali jakousi numerologii nebo uctívání čísel a každé číslo považovali za číslo s vlastním charakterem a významem. Například číslo jedna bylo generátorem všech čísel, dvojka představovala názor, trojka harmonii, čtyřka spravedlnost, pětka manželství, šestka stvoření, sedmička sedm planet neboli „putujících hvězd“ atd. Lichá čísla byla považována za ženská a sudá za mužská.
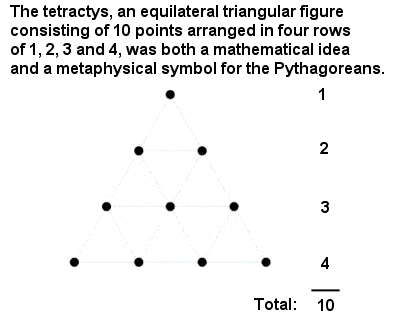
Pythagorejská tetraktida
Nejsvětějším ze všech čísel byla „tetraktida“ neboli desítka, trojúhelníkové číslo složené ze součtu jedničky, dvojky, trojky a čtyřky. Je velkou poctou intelektuálním úspěchům pýthagorejců, že zvláštní místo čísla 10 odvodili z abstraktního matematického argumentu, a nikoli z něčeho tak přízemního, jako je počítání prstů na dvou rukou.
Pýthagorás a jeho škola – stejně jako hrstka dalších matematiků starověkého Řecka – se však do značné míry zasloužili o zavedení přísnější matematiky, než byla ta předchozí, která vycházela z prvních principů s využitím axiomů a logiky. Před Pythagorem byla například geometrie pouhým souborem pravidel odvozených empirickým měřením.
Pythagoras objevil, že lze vytvořit úplný matematický systém, kde geometrické prvky odpovídají číslům a kde celá čísla a jejich poměry jsou vše, co je nutné k vytvoření celého systému logiky a pravdy.
Pythagorova věta
Je připomínán především díky tomu, co se stalo známým jako Pythagorova věta (nebo Pythagorova věta): že pro libovolný pravoúhlý trojúhelník se čtverec délky přepony (nejdelší strany, která leží naproti pravému úhlu) rovná součtu čtverců ostatních dvou stran (nebo „ramen“).
Zapsáno jako rovnice: a2 + b2 = c2.
Pythagoras a jeho následovníci si neuvědomili, že to platí i pro libovolný tvar: plocha pětiúhelníku na přeponě se tedy rovná součtu pětiúhelníků na ostatních dvou stranách, stejně jako pro půlkruh nebo jakýkoli jiný pravidelný (nebo dokonce nepravidelný( tvar.
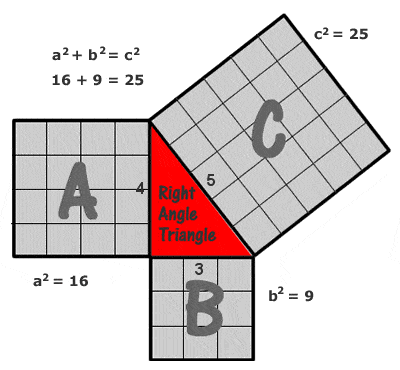
Pythagorova (Pythagorova) věta
Nejjednodušším a nejčastěji uváděným příkladem pythagorejského trojúhelníku je trojúhelník se stranami 3, 4 a 5 jednotek (32 + 42 = 52. V tomto případě se jedná o trojúhelník se stranami o délce 5 jednotek, jak je vidět po nakreslení sítě jednotkových čtverců na každé straně jako na obrázku vpravo), ale existuje potenciálně nekonečné množství dalších celočíselných „pythagorovských trojúhelníků“, počínaje (5, 12 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41) atd. Je však třeba poznamenat, že (6, 8, 10) není takzvanou „primitivní“ pythagorovskou trojicí, protože je jen násobkem (3, 4, 5).
Pythagorova věta a vlastnosti pravoúhlých trojúhelníků se zdá být nejstarším a nejrozšířenějším matematickým vývojem po základní aritmetice a geometrii a dotýkají se jí některé nejstarší matematické texty z Babylonu a Egypta, pocházející z doby před více než tisíci lety. Jeden z nejjednodušších důkazů pochází ze staré Číny a pravděpodobně pochází z doby daleko před Pythagorovým narozením. Byl to však právě Pythagoras, kdo dal větě definitivní podobu, i když není jasné, zda ji Pythagoras sám definitivně dokázal, nebo ji pouze popsal. Ať tak či onak, stala se jednou z nejznámějších matematických vět a dnes existuje až 400 různých důkazů, některé geometrické, některé algebraické, některé zahrnující pokročilé diferenciální rovnice atd.
Brzy se však ukázalo, že jsou možná i neceločíselná řešení, takže například rovnoramenný trojúhelník se stranami 1, 1 a √2 má také pravý úhel, jak zjistili Babylóňané o několik století dříve. Když se však Pythagorův žák Hippasus pokusil vypočítat hodnotu √2, zjistil, že ji nelze vyjádřit jako zlomek, čímž naznačil potenciální existenci zcela nového světa čísel, iracionálních čísel (čísel, která nelze vyjádřit jako jednoduché zlomky celých čísel). Tento objev poněkud rozbil elegantní matematický svět vybudovaný Pythagorem a jeho následovníky a existence čísla, které nelze vyjádřit jako poměr dvou božích výtvorů (tak uvažovali o celých číslech), ohrozila celý systém víry tohoto kultu.
Ubohý Hippasus byl zřejmě tajnůstkářskými pythagorejci utopen za to, že tento důležitý objev odvysílal do okolního světa. Nahrazení představy o božskosti celých čísel bohatším pojmem kontinua však bylo zásadním vývojem v matematice. Znamenalo to skutečný zrod řecké geometrie, která se zabývá přímkami, rovinami a úhly, které jsou spojité, nikoli diskrétní.
Mezi dalšími úspěchy v geometrii si Pythagoras (nebo alespoň jeho následovníci, pythagorejci) také uvědomil, že součet úhlů trojúhelníku je roven dvěma pravým úhlům (180°), a pravděpodobně také zobecnění, které říká, že součet vnitřních úhlů mnohoúhelníku o n stranách je roven (2n – 4) pravým úhlům a že součet jeho vnějších úhlů je roven 4 pravým úhlům. Dokázali sestrojit obrazce o dané ploše a používat jednoduchou geometrickou algebru, například řešit rovnice typu a(a – x) = x2 geometrickými prostředky.
Pythagorejci také položili základy teorie čísel, když zkoumali trojúhelníková, čtvercová a také dokonalá čísla (čísla, která jsou součtem svých dělitelů). Objevili několik nových vlastností čtvercových čísel, například že kvadrát čísla n je roven součtu prvních n lichých čísel (např. 42 = 16 = 1 + 3 + 5 + 7). Objevili také alespoň první dvojici soudělných čísel, 220 a 284 (soudělná čísla jsou dvojice čísel, u nichž se součet dělitelů jednoho čísla rovná druhému číslu, např. vlastní dělitelé čísla 220 jsou 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 a 110, jejichž součet je 284; a vlastní dělitelé čísla 284 jsou 1, 2, 4, 71 a 142, jejichž součet je 220).
Hudební teorie
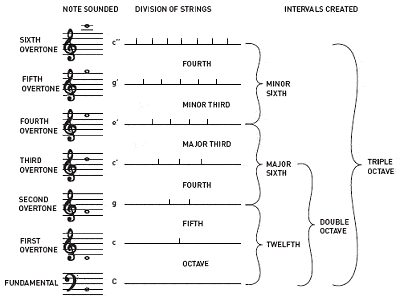
Pythagorovi se připisuje objev poměrů mezi harmonickými hudebními tóny
Pythagorovi se rovněž připisuje objev, že intervaly mezi harmonickými hudebními tóny mají vždy celočíselné poměry. Například zahrání poloviny délky kytarové struny dává stejný tón jako otevřená struna, ale o oktávu vyšší; třetina délky dává jiný, ale harmonický tón; atd.
Naopak poměry necelých čísel mají tendenci dávat disonantní zvuky. Tímto způsobem popsal Pythagoras první čtyři overtony, které vytvářejí společné intervaly, jež se staly základními stavebními kameny hudební harmonie: oktávu (1:1), dokonalou kvintu (3:2), dokonalou kvartu (4:3) a velkou tercii (5:4). Nejstarší způsob ladění dvanáctitónové chromatické stupnice je znám jako pythagorejské ladění a vychází z hromady dokonalých kvint, z nichž každá je laděna v poměru 3:2.
Mystický Pythagoras byl tímto objevem tak nadšen, že nabyl přesvědčení, že celý vesmír je založen na číslech a že planety a hvězdy se pohybují podle matematických rovnic, které odpovídají hudebním tónům, a vytvořil tak jakousi symfonii, „Musical Universalis“ neboli „Hudbu sfér“.
| << Zpět k řecké matematice | Před Platonem >> |
.
