V této části se seznámíme s množinovými operacemi a zápisy, abychom mohli tyto pojmy aplikovat na početní i pravděpodobnostní úlohy. Začneme definicí některých pojmů.
Množina je soubor objektů a její členy nazýváme prvky množiny. Množinu pojmenováváme velkými písmeny a její členy uzavíráme do kudrnatých závorek. Předpokládejme, že potřebujeme vypsat členy šachového klubu. Použijeme následující zápis množiny:
C ={Ken, Bob, Tran, Shanti, Eric}
Množina, která nemá žádné členy, se nazývá prázdná množina. Prázdná množina se označuje symbolem Ø.
Dvě množiny jsou si rovny, jestliže mají stejné prvky.
Množina A je podmnožinou množiny B, jestliže každý člen A je zároveň členem B.
Předpokládejme, že C = {Al, Bob, Chris, David, Ed} a A = {Bob, David}. Pak A je podmnožinou množiny C, zapisuje se jako 
.
Každá množina je podmnožinou sebe sama a prázdná množina je podmnožinou každé množiny.
Sjednocení dvou množin
Nechť A a B jsou dvě množiny, pak sjednocení A a B, zapisuje se jako 
, je množina všech prvků, které jsou buď v A, nebo v B, nebo v A i v B.
Každá množina je podmnožinou sebe sama a prázdná množina je podmnožinou každé množiny.
Průnik dvou množin
Nechť A a B jsou dvě množiny, pak průnik A a B, zapsaný jako 
, je množina všech prvků, které jsou společné oběma množinám A i B.
Univerzální množina U je množina složená ze všech uvažovaných prvků.
Komplement množiny
Nechť A je libovolná množina, pak komplement množiny A, zapsaný jako 
, je množina složená z prvků univerzální množiny U, které v A nejsou.
Disjunktní množiny
Dvě množiny A a B se nazývají disjunktní množiny, je-li jejich průnikem prázdná množina.
= {Jackson, Sanders}
= {Aikman, Griffey, Jackson, Rice, Sanders, Thomas, Young}
= {oranžová, zelená, indigová, fialová}Pro lepší pochopení předpokládejme, že univerzální množina U představuje barvy spektra a P základní barvy, pak představuje ty barvy spektra, které nejsou základními barvami.
.
= {červená, žlutá, modrá, zelená}
= {oranžová, indigová, fialová}
= {červená, žlutá, modrá, fialová} = {fialová}Vennovy diagramy
Vennovy diagramy nyní použijeme k znázornění vztahů mezi množinami. Na konci 19. století vyvinul anglický logik John Venn metodu pro znázornění vztahů mezi množinami. Tyto vztahy znázornil pomocí diagramů, které jsou dnes známé jako Vennovy diagramy. Vennův diagram představuje množinu jako vnitřek kruhu. Často jsou dva nebo více kruhů uzavřeny v obdélníku, kde obdélník představuje univerzální množinu. Vizualizovat průnik nebo sjednocení množiny je snadné. V této části budeme Vennovy diagramy používat hlavně k třídění různých množin a počítání objektů.
|
(a) |
(b) |
(c) |
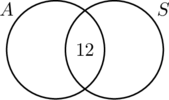
Protože 30 lidí řídilo auta s automatickou převodovkou, musí kruh A obsahovat 30 prvků. To znamená, že x + 12 = 30, nebo x = 18. Podobně, protože 20 lidí řídilo auta se standardní převodovkou, musí kruh B obsahovat 20 prvků, neboli y +12 = 20, což zase znamená, že y = 8.
Teď, když jsou všechny informace seřazeny, lze z diagramu snadno vyčíst, že 18 lidí řídilo pouze auta s automatickou převodovkou, 12 lidí řídilo oba typy aut a 8 lidí řídilo pouze auta se standardní převodovkou. Průzkumu se tedy zúčastnilo 18 + 12 + 8 = 38 lidí.
|
(a) |
(b) |
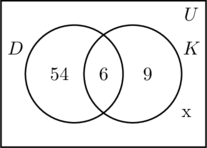
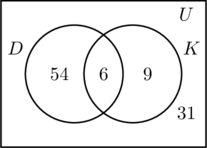
Tři oblasti spojené s množinami D a K vyplníme stejným způsobem jako dříve. Protože se průzkumu zúčastnilo 100 osob, musí obdélník představující univerzální množinu U obsahovat 100 objektů. Nechť x představuje ty lidi v univerzální množině, kteří nejsou ani v množině D, ani v K. To znamená, že 54 + 6 + 9 + x = 100, neboli x = 31.
V průzkumu tedy bylo 31 lidí, kteří nenavštívili ani jedno místo.
- 50 běhá, 30 plave a 35 jezdí na kole
- 14 běhá a plave
- 7 plave a jezdí na kole
- 9 běhá a jezdí na kole
- 3 lidé se účastní všech tří aktivit
Řešení
|
(a) |
(b) |
(c) . |
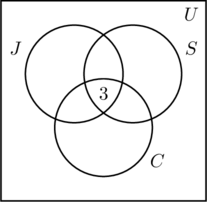
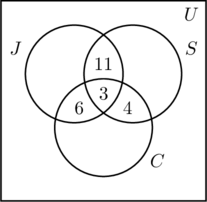
Do nejvnitřnější oblasti obrázku (a) umístíme trojku, protože představuje počet osob, které se účastní všech tří činností. Dále vypočítáme x, y a z.
- Protože 14 lidí běhá a plave, x +3 = 14, neboli x = 11. To znamená, že x = 11.
- Z toho, že 9 lidí běhá a jezdí na kole, vyplývá, že y + 3 = 9, neboli y = 6.
- Protože 7 lidí plave a jezdí na kole, z + 3 = 7, neboli z = 4.
- Tato informace je znázorněna na obrázku (b).
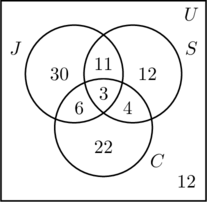
- Protože 50 lidí běhá, m + 11 + 6 + 3 = 50, neboli m = 30. To znamená, že m + 11 + 6 + 3 = 50, neboli m = 30.
- 30 lidí plave, proto n + 11 + 4 + 3 = 30, neboli n = 12.
- 35 lidí jezdí na kole, proto p + 6 + 4 + 3 = 35, neboli p = 22.
- Na kole jezdí 30 lidí.
- Složením všech zápisů ve všech třech množinách dostaneme součet 88.
- Podíváme-li se, kolik lidí je ve všech třech množinách, dostaneme součet 88. Protože bylo dotazováno 100 lidí, počet uvnitř univerzální množiny, ale mimo všechny tři množiny, je 100 – 88, tedy 12.
- Na obrázku c) jsou informace uspořádány a na otázky lze snadno odpovědět.
Praktické otázky
1. Jaké jsou výsledky? Nechť univerzální množina U = {a, b, c, d, e, f, g, h, i, j},V = {a, e, i, f, h} a W = {a, c, e, g, i}. Vypište členy následujících množin:
a. 
b. 
2. Uvažujte následující množiny: A = {SARS, H1N1, H5N1, MERS-CoV, COVID-19, chřipka, norovirus}, B = {Listerie, Campylobacter, Salmonella, E. coli O157, Norovirus, Shigella} a C = {SARS, Listerie, Tuberkulóza, H5N1, Salmonella, HIV, COVID-19}. Vyjmenujte členy následujících souborů:
a. 
b. 
3. Průzkum mezi sportovci ukázal, že na drobné bolesti užívá 30 z nich aspirin, 50 ibuprofen a 15 obojí. Všichni dotazovaní sportovci používali alespoň jeden z obou léků proti bolesti. Kolik sportovců bylo dotazováno?“
4. Studie 150 středoškoláků zjistila, že 25 z nich uvedlo, že v minulosti prodělalo otřes mozku nebo úraz hlavy, 52 uvedlo, že zažilo duševní onemocnění, a 15 uvedlo oba následky. Kolik studentů neuvedlo ani jeden z těchto následků?
5. Jaké jsou výsledky studie? Průzkum mezi 100 studenty Ryersonovy univerzity zjistil, že 50 z nich odebírá službu Netflix, 40 Amazon Prime a 30 Disney+. Z nich 15 si předplácí Netflix i Amazon Prime, 10 Amazon Prime i Disney+, 10 Netflix i Disney+ a 5 má všechny tři předplacené služby. Nakreslete Vennův diagram a určete následující:
a. Počet studentů, kteří mají předplacenou službu Amazon Prime, ale nemají ostatní dvě streamovací služby.
b. Počet studentů, kteří si předplácejí službu Netflix nebo Amazon Prime, ale ne službu Disney+.
c. Počet studentů, kteří si nepředplácejí žádnou z těchto služeb.
.