Grupa 
je konečná nebo nekonečná množina prvků spolu s binární operací (tzv. grupová operace), které společně splňují čtyři základní vlastnosti: uzavřenost, asociativitu, vlastnost identity a inverzní vlastnost. Operace, vzhledem k níž je grupa definována, se často nazývá „grupová operace“ a o množině se říká, že je grupou „pod“ touto operací. Prvky 
, 
, 
, … s binární operací mezi 
a 
označené 
tvoří grupu, jestliže
1. Uzávěr: Jestliže 
a 
jsou dva prvky v 
, pak součin 
je také v 
.
2. Asociativita: Definované násobení je asociativní, tj. pro všechny 
, 
.
3. Identita: Existuje identitní prvek 
(alias 1, 
nebo 
) takový, že 
pro každý prvek 
.
4. Inverzní: Ke každému prvku musí existovat inverzní (neboli reciproční) prvek. Proto pro každý prvek 
z 
obsahuje množina prvek 
takový, že 
.
Grupa je monoid, jehož každý prvek je inverzní.
Grupa musí obsahovat alespoň jeden prvek, přičemž jedinečná (až na izomorfismus) jednoprvková skupina se nazývá triviální skupina.
Studium grup se nazývá teorie grup. Pokud existuje konečný počet prvků, nazývá se grupa konečnou grupou a počet prvků se nazývá řád grupy. Podmnožina grupy, která je uzavřená při grupové operaci a inverzní operaci, se nazývá podgrupa. Podskupiny jsou také grupy a mnohé běžně se vyskytující grupy jsou ve skutečnosti speciálními podgrupami nějaké obecnější větší grupy.
Základním příkladem konečné grupy je symetrická grupa 
, což je grupa permutací (neboli „pod permutací“) objektů 
. Nejjednodušší nekonečnou grupou je množina celých čísel při obvyklém sčítání. Pro spojité grupy lze uvažovat reálná čísla nebo množinu 
inverzních matic. Poslední dvě jmenované jsou příklady Lieových grup.
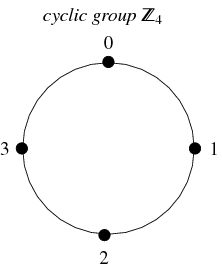
Jedním z velmi častých typů grup jsou cyklické grupy. Tato grupa je izomorfní ke grupě celých čísel (modulo 
), značí se 
, 
nebo 
a je definována pro každé celé číslo 
. Je uzavřená při sčítání, asociativní a má jedinečné inverze. Její prvky představují čísla od 0 do 
, přičemž prvek identity představuje 0 a inverzní prvek 
představuje 
.
Mapa mezi dvěma grupami, která zachovává identitu a grupovou operaci, se nazývá homomorfismus. Má-li homomorfismus inverzi, která je také homomorfismem, pak se nazývá izomorfismus a obě grupy se nazývají izomorfní. Dvě grupy, které jsou navzájem izomorfní, se považují za „stejné“, pokud se na ně díváme jako na abstraktní grupy. Například grupa rotací čtverce, znázorněná na obrázku níže, je cyklická grupa 
.
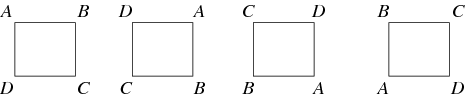
Ogrupová akce obecně mluvíme tehdy, když grupa působí na množinu, permutuje její prvky, takže mapa z grupy na permutační grupu množiny je homomorfismus. Například rotace čtverce jsou podgrupou permutací jeho rohů. Jedním z důležitých grupových dějů pro každou grupu 
je její působení na sebe sama konjugací. To jsou jen některé z možných grupových automorfismů. Dalším důležitým druhem grupového působení je grupové zobrazení, kdy grupa působí na vektorový prostor pomocí inverzních lineárních map. Je-li polem vektorového prostoru komplexní číslo, nazývá se někdy zobrazení CG modul.
Grupová působení, a zejména zobrazení, jsou velmi důležitá v aplikacích nejen v teorii grup, ale také ve fyzice a chemii. Protože grupu lze považovat za abstraktní matematický objekt, může se stejná grupa vyskytovat v různých souvislostech. Je proto užitečné uvažovat o reprezentaci grupy jako o jednom konkrétním vtělení grupy, která může mít i jiné reprezentace. Neredukovatelné zobrazení grupy je takové zobrazení, pro které neexistuje žádná unitární transformace, která by transformovala matici zobrazení do blokové diagonální formy. Neredukovatelná zobrazení mají řadu pozoruhodných vlastností, které jsou formalizovány v teorému o ortogonalitě grupy
.