Fyzika

Cíle učení

Na konci této části budete schopni:

• Popsat typický experiment s fotoelektrickým jevem.
• Určit maximální kinetickou energii fotoelektronů vyvržených fotony o jedné energii nebo vlnové délce, je-li dána maximální kinetická energie fotoelektronů pro jinou energii nebo vlnovou délku fotonu.

Obrázek 1. Fotoelektrický jev lze pozorovat tak, že necháte dopadat světlo na kovovou desku v této evakuované trubici. Elektrony vyražené světlem se shromažďují na sběrném vodiči a měří se jako proud. Zpomalovací napětí mezi kolektorovým drátem a deskou lze pak nastavit tak, aby se určila energie vyvržených elektronů. Pokud je například dostatečně záporné, nedostanou se na vodič žádné elektrony. (kredit: P.P. Urone)

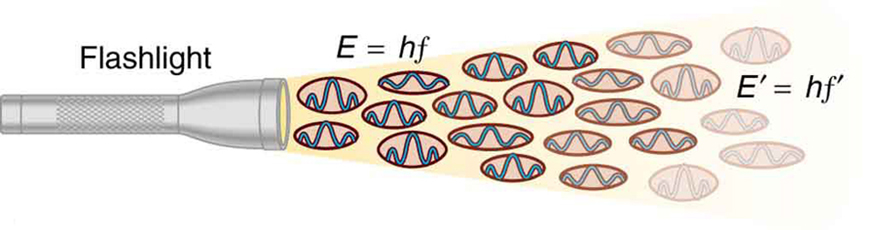
Obrázek 2. EM vlna o frekvenci f se skládá z fotonů neboli jednotlivých kvant EM záření. Energie každého fotonu je E = hf, kde h je Planckova konstanta a f je frekvence EM záření. Vyšší intenzita znamená více fotonů na jednotku plochy. Svítilna vyzařuje velké množství fotonů o mnoha různých frekvencích, tudíž další mají energii E′ = hf′, a tak dále.

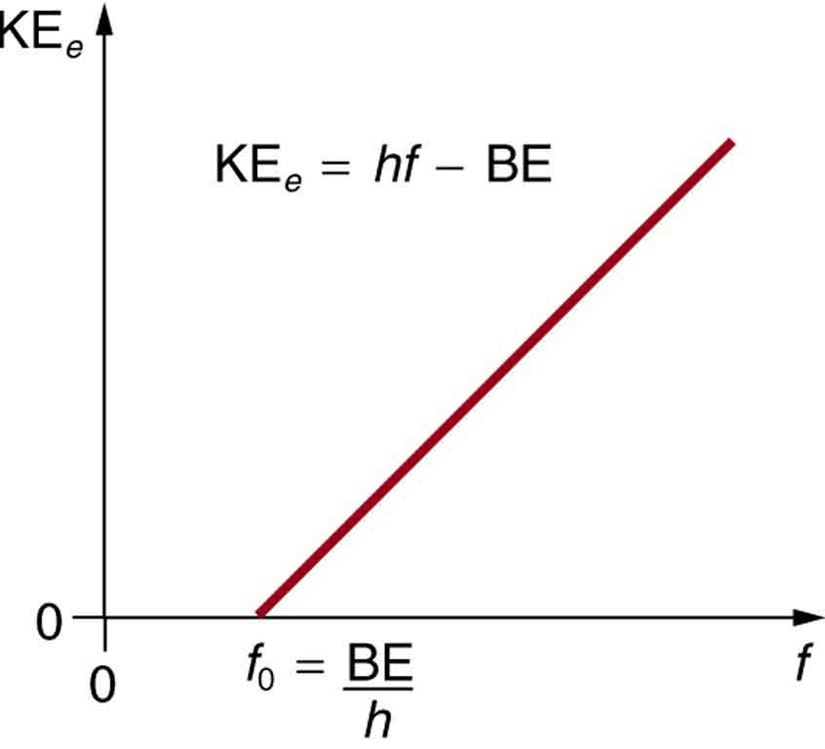
Obr. 3. Fotoelektrický jev. Graf závislosti kinetické energie vyvrženého elektronu KEe na frekvenci EM záření dopadajícího na určitý materiál. Existuje prahová frekvence, pod kterou nejsou vyvrženy žádné elektrony, protože jednotlivý foton interagující s jednotlivým elektronem nemá dostatečnou energii k jeho odtržení. Nad prahovou energií roste KEe lineárně s f, což odpovídá vztahu KEe = hf – BE. Sklon této přímky je h – údaje lze použít k experimentálnímu určení Planckovy konstanty. Einstein podal první úspěšné vysvětlení těchto údajů tím, že navrhl myšlenku fotonů – kvant EM záření.

Příklad č. 1. Výpočet energie fotonu a fotoelektrického jevu: Fialové světlo

1. Jaká je energie fotonu 420nm fialového světla v joulech a elektronvoltech?

2. Jaká je maximální kinetická energie elektronů vyvržených z vápníku 420nm fialovým světlem za předpokladu, že vazebná energie (neboli pracovní funkce) elektronů pro kovový vápník je 2,71 eV?

Strategie

Pro řešení části 1 si uvědomte, že energie fotonu je dána vztahem E = hf. Pro část 2 platí, že jakmile je energie fotonu vypočtena, je pro nalezení maximální kinetické energie vyvrženého elektronu jednoduchá aplikace KEe = hf – BE, protože BE je dána.

Řešení části 1

Energie fotonu je dána vztahem E = hf.

Protože je dána vlnová délka, nikoli frekvence, řešíme známý vztah c = fλ pro frekvenci, čímž získáme f=\frac{c}{\lambda}\.

Spojením těchto dvou rovnic získáme užitečný vztah E=\frac{hc}{\lambda}\\.

Nyní dosazením známých hodnot získáme

\displaystyle{E}=\frac{\left(6,63\times10^{-34}\text{ J}\cdot\text{ s}\right)\left(3.00\times10^{8}\text{ m/s}\right)}{420\times10^{-9}\text{ m}}=4,74\times10^{-19}\text{ J}\

Převodem na eV je energie fotonu

\displaystyle{E}=\left(4.47\times10^{-19}\text{ J}\pravá)\frac{1\text{ eV}}{1,6\times10^{-19}\text{ J}}=2,96\text{ eV}\

Řešení pro část 2

Zjištění kinetické energie vyvrženého elektronu je nyní jednoduchou aplikací rovnice KEe = hf – BE. Dosazením energie fotonu a vazebné energie získáme KEe = hf – BE = 2,96 eV – 2,71 eV = 0,246 eV.

Diskuse

Energie tohoto 420nm fotonu fialového světla je nepatrný zlomek joulu, a tak není divu, že by pro nás bylo obtížné jeden foton přímo vnímat – lidé jsou spíše přizpůsobeni energiím v řádu joulů. Podíváme-li se však na energii v elektronvoltech, zjistíme, že tento foton má dostatek energie, aby ovlivnil atomy a molekuly. Například molekulu DNA lze rozbít energií přibližně 1 eV a typické energie atomů a molekul se pohybují v řádu eV, takže UV foton v tomto příkladu může mít biologické účinky. Vyhozený elektron (nazývaný fotoelektron) má poměrně nízkou energii a necestoval by daleko, leda ve vakuu. Elektron by byl zastaven zpomalujícím potenciálem o hodnotě pouhých 0,26 eV. Pokud by totiž vlnová délka fotonu byla delší a jeho energie menší než 2,71 eV, pak by vzorec udával zápornou kinetickou energii, což je nemožné. To jednoduše znamená, že fotony o vlnové délce 420 nm s energií 2,96 eV nejsou o mnoho vyšší než prahová frekvence. Sami si můžete ukázat, že prahová vlnová délka je 459 nm (modré světlo). To znamená, že pokud se ve světelném měřiči použije kovový vápník, bude měřič necitlivý na vlnové délky delší než vlnové délky modrého světla. Takový světloměr by byl například zcela necitlivý na červené světlo.

PhET Explorations:

Podívejte se, jak světlo vyrazí elektrony z kovového terče, a zopakujte si experiment, který dal vzniknout oboru kvantové mechaniky.

Klikněte pro stažení simulace. Spusťte pomocí Javy.

Shrnutí oddílu

• Fotoelektrický jev je proces, při kterém EM záření vyvrhuje elektrony z materiálu.
• Einstein navrhl fotony jako kvanta EM záření s energií E = hf, kde f je frekvence záření.
• Všechno EM záření se skládá z fotonů. Jak Einstein vysvětlil, všechny vlastnosti fotoelektrického jevu jsou způsobeny interakcí jednotlivých fotonů s jednotlivými elektrony.
• Maximální kinetická energie KEe vyvržených elektronů (fotoelektronů) je dána vztahem KEe = hf – BE, kde hf je energie fotonu a BE je vazebná energie (nebo pracovní funkce) elektronu na daný materiál.

Pojmové otázky

1. Je viditelné světlo jediným typem elektromagnetického záření, které může způsobit fotoelektrický jev?
2. Které aspekty fotoelektrického jevu nelze vysvětlit bez fotonů? Které lze vysvětlit bez fotonů? Jsou tyto aspekty v rozporu s existencí fotonů?
3. Je fotoelektrický jev přímým důsledkem vlnové povahy EM záření nebo částicové povahy EM záření? Vysvětlete stručně.
4. Izolátory (nekovy) mají vyšší BE než kovy a pro fotony je obtížnější vytlačit elektrony z izolátorů. Diskutujte, jak to souvisí s volnými náboji v kovech, které z nich dělají dobré vodiče.
5. Pokud zvednete a zatřesete kusem kovu, který má v sobě elektrony volně se pohybující jako proud, žádné elektrony nevypadnou. Přesto pokud kov zahřejete, elektrony se mohou vyvařit. Vysvětlete obě tyto skutečnosti tak, jak souvisejí s množstvím a rozložením energie při otřásání předmětu ve srovnání s jeho zahříváním.

Problémy & Cvičení

1. Jaká je nejdelší vlnová délka EM záření, které může ze stříbra vyrazit fotoelektron, za předpokladu, že vazebná energie je 4,73 eV? Je to ve viditelném oboru?“
2. Najděte nejdelší vlnovou délku fotonu, který může vymrštit elektron z draslíku za předpokladu, že vazebná energie je 2,24 eV. Je to viditelné EM záření?
3. Jaká je vazebná energie v eV elektronů v hořčíku, jestliže nejdelší vlnová délka fotonu, který může vyrazit elektrony, je 337 nm?
4. Vypočítejte vazebnou energii v eV elektronů v hliníku, jestliže nejdelší vlnová délka fotonu, který je může vyrazit, je 304 nm.
5. Jaká je maximální kinetická energie v eV elektronů vyvržených z kovu sodíku EM zářením o vlnové délce 450 nm, je-li vazebná energie 2,28 eV?
6. UV záření o vlnové délce 120 nm dopadá na kov zlata, na který jsou elektrony vázány 4,82 eV. Jaká je maximální kinetická energie vyvržených fotoelektronů?
7. Fialové záření o vlnové délce 400 nm vyvrhuje z kovu sodíku elektrony s maximální kinetickou energií 0,860 eV. Jaká je vazebná energie elektronů na kov sodíku?
8. UV záření o vlnové délce 300 nm dopadá na kov uranu a vyvrhuje elektrony o kinetické energii 0,500 eV. Jaká je vazebná energie elektronů na kovový uran?
9. (a) Jaká je vlnová délka EM záření, které z kovového vápníku vymrští elektrony o energii 2,00 eV, za předpokladu, že vazebná energie je 2,71 eV? (b) O jaký typ EM záření se jedná?
10. Najděte vlnovou délku fotonů, které z kovu draslíku vymrští elektrony o energii 0,100 EV, za předpokladu, že vazebná energie je 2,24 eV. Jsou tyto fotony viditelné?
11. Jaká je maximální rychlost elektronů vyvržených z materiálu fotony o vlnové délce 80 nm, jestliže jsou na materiál vázány energií 4,73 eV?
12. Fotoelektrony z materiálu s vazebnou energií 2,71 eV jsou vyvrženy fotony o vlnové délce 420 nm. Za jak dlouho po vyražení urazí tyto elektrony vzdálenost 2,50 cm k detekčnímu zařízení?
13. Na kovový vápník je promítán laser o výkonu 2,00 mW při vlnové délce 400 nm. (a) Kolik elektronů za sekundu je vyvrženo? (b) Jaký výkon odnesou elektrony za předpokladu, že vazebná energie je 2,71 eV?
14. (a) Vypočítejte počet fotoelektronů za sekundu vyvržených z plochy 1,00 mm2 kovu sodíku EM zářením o vlnové délce 500 nm a intenzitě 1,30 kW/m2 (intenzita slunečního záření nad zemskou atmosférou). (b) Vzhledem k tomu, že vazebná energie je 2,28 eV, jaký výkon odnesou elektrony? (c) Elektrony odnesou méně energie, než kolik jí přinesou fotony. Kam odchází další energie? Jak ji lze získat zpět?“
15. Nerozumné výsledky. Červené světlo o vlnové délce 700 nm se promítá na kovový hořčík, na který jsou vázány elektrony o energii 3,68 eV. (a) Pomocí KEe = hf – BE vypočítejte kinetickou energii vyvržených elektronů. (b) Co je na tomto výsledku nesmyslného? (c) Které předpoklady jsou nerozumné nebo nekonzistentní?“
16. Nerozumné výsledky. (a) Jaká je vazebná energie elektronů na materiál, z něhož jsou elektrony o energii 4,00 EV vyvrženy EM zářením o vlnové délce 400 nm? (b) Co je na tomto výsledku nesmyslného? (c) Které předpoklady jsou nerozumné nebo nekonzistentní?

Slovníček

fotoelektrický jev: jev, při kterém některé materiály vyvrhují elektrony, když na ně svítíme

foton: kvantum nebo částice elektromagnetického záření

fotonová energie: E = hf

fotonová energie: nazývá se také pracovní funkce; množství energie potřebné k vyražení elektronu z materiálu

.