Fázový diagram vody
Obrázek 11.23 „Dvě verze fázového diagramu vody“ ukazuje fázový diagram vody a ilustruje, že trojný bod vody nastává při 0,01 °C a 0,00604 atm (4,59 mmHg). Trojný bod (273,16 K) je mnohem reprodukovatelnější než bod tání ledu, který závisí na množství rozpuštěného vzduchu a atmosférickém tlaku, a používá se k definování absolutní (kelvinovské) teplotní stupnice. Trojný bod také představuje nejnižší tlak, při kterém může kapalná fáze existovat v rovnováze s pevnou látkou nebo párou. Při tlaku nižším než 0,00604 atm se tedy led při zvyšování teploty nerozpouští na kapalinu; pevná látka přímo sublimuje na vodní páru. Sublimaci vody při nízké teplotě a tlaku lze využít k „lyofilizaci“ potravin a nápojů. Potravina nebo nápoj se nejprve zchladí na teplotu pod bodem mrazu a umístí se do nádoby, ve které se udržuje tlak nižší než 0,00604 atm. Poté se při zvyšování teploty voda sublimuje a zůstane dehydrovaná potravina (např. ta, kterou používají baťůžkáři nebo astronauti) nebo nápoj v prášku (jako u lyofilizované kávy).
Fázový diagram pro vodu znázorněný v části b) na obrázku 11.23 „Dvě verze fázového diagramu vody“ ukazuje hranici mezi ledem a vodou v rozšířeném měřítku. Křivka tání ledu se svažuje nahoru a mírně doleva, nikoli nahoru a doprava jako na obrázku 11.22 „Typický fázový diagram pro látku, která vykazuje tři fáze – pevnou, kapalnou a plynnou – a nadkritickou oblast“; to znamená, že teplota tání ledu klesá s rostoucím tlakem; při 100 MPa (987 atm) led taje při -9 °C. Voda se takto chová proto, že je jednou z mála známých látek, u nichž má krystalická pevná látka menší hustotu než kapalina (mezi další patří antimon a vizmut). Zvyšování tlaku ledu, který je v rovnováze s vodou při 0 °C a 1 atm, má tendenci tlačit některé molekuly blíže k sobě, čímž se zmenšuje objem vzorku. Zmenšení objemu (a odpovídající zvýšení hustoty) je u pevné látky nebo kapaliny menší než u plynu, ale stačí k roztavení části ledu.
Obrázek 11.23 Dvě verze fázového diagramu vody
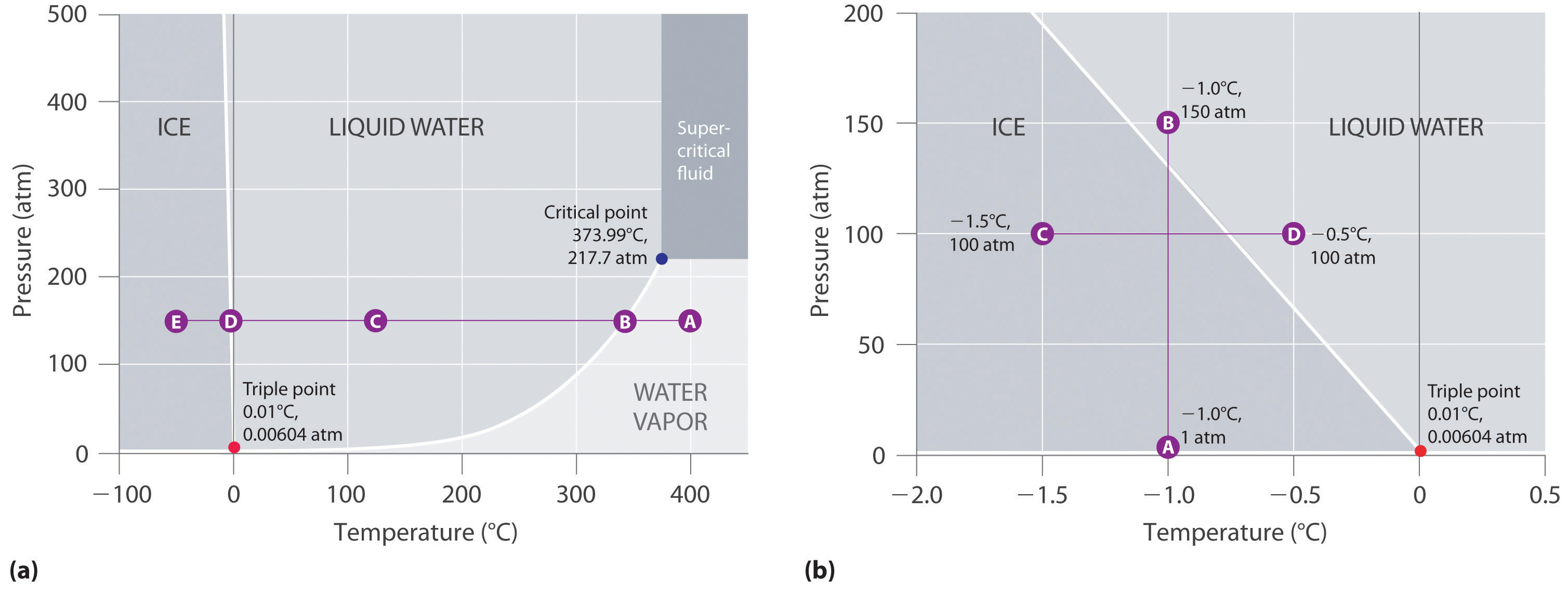
(a) V tomto grafu s lineárními osami teploty a tlaku je hranice mezi ledem a kapalnou vodou téměř svislá. (b) Tento graf s rozšířenou stupnicí znázorňuje pokles teploty tání s rostoucím tlakem. (Písmena odkazují na body probírané v příkladu 10.)
V části (b) na obrázku 11.23 „Dvě verze fázového diagramu vody“ se bod A nachází při P = 1 atm a T = -1,0 °C v pevné (ledové) oblasti fázového diagramu. Když se tlak zvýší na 150 atm, zatímco teplota zůstane stejná, přímka z bodu A protne hranici mezi ledem a vodou do bodu B, který leží v oblasti kapalné vody. Z toho vyplývá, že při tlaku 150 atm se led při teplotě -1,0 °C rozpustí. Již jsme naznačili, že závislost teploty tání vody na tlaku má zásadní význam. Kdyby se hranice mezi pevnou a kapalnou látkou ve fázovém diagramu vody skláněla spíše nahoru a doprava než doleva, led by byl hustší než voda, kostky ledu by se potápěly, vodovodní potrubí by při zamrznutí nepraskalo a nemrznoucí směs v automobilových motorech by byla zbytečná.
Do nedávna se v mnoha učebnicích popisovalo bruslení na ledě jako možné, protože tlak vytvářený bruslařovým nožem je dostatečně vysoký na to, aby roztál led pod nožem, a tím se vytvořila mazací vrstva kapalné vody, která umožňuje bruslaři klouzat po ledu. Ačkoli je toto vysvětlení intuitivně uspokojivé, je nesprávné, jak můžeme ukázat jednoduchým výpočtem. Připomeňme si z kapitoly 10 „Plyny“, že tlak (P) je síla (F) působící na jednotku plochy (A):
rovnice 11.4
P = F A
Pro výpočet tlaku, který bruslař vyvíjí na led, musíme vypočítat pouze působící sílu a plochu nože brusle. Předpokládáme-li bruslaře o hmotnosti 75,0 kg (165 lb), pak síla, kterou bruslař působí na led vlivem gravitace, je
rovnice 11.5
F = mg
kde m je hmotnost a g je zrychlení způsobené zemskou gravitací (9,81 m/s2). Síla je tedy
Rovnice 11.6
F = (75,0 kg)(9,81 m/s2) = 736 (kg-m)/s2 = 736 N
Předpokládáme-li, že nože brusle jsou 2.0 mm široké a 25 cm dlouhé, pak plocha spodní části každého nože je
Rovnice 11.7
A = (2,0 × 10-3 m)(25 × 10-2 m) = 5.0 × 10-4 m2
Pokud bruslař klouže po jedné noze, tlak působící na led je
rovnice 11.8
P = 736 N 5,0 × 10 – 4 m 2 = 1,5 × 10 6 N/m 2 = 1.5 × 10 6 Pa = 15 atm
Tlak je mnohem nižší než tlak potřebný ke snížení teploty tání ledu dokonce o 1 °C a zkušenosti ukazují, že bruslit lze i při teplotě hluboko pod bodem mrazu. Tlakem vyvolané tání ledu tedy nemůže vysvětlit nízké tření, které umožňuje bruslařům (a hokejovým pukům) klouzat. Nejnovější výzkumy ukazují, že povrch ledu, kde se setkává uspořádaná soustava molekul vody se vzduchem, se skládá z jedné nebo více vrstev téměř tekuté vody. Zdá se, že tyto vrstvy spolu s táním vyvolaným třením, když se bruslař tlačí vpřed, vysvětlují jak snadnost, s jakou bruslař klouže, tak skutečnost, že bruslení se stává obtížnějším při teplotách nižších než přibližně -7 °C, kdy se počet mazacích povrchových vodních vrstev snižuje.
.
