Věda > Fyzika > Fotoelektrický jev >Einsteinova fotoelektrická rovnice
V tomto článku odvodíme Einsteinovu fotoelektrickou rovnici a prozkoumáme její použití k ověření vlastností fotoelektrického jevu světla.
Vlnová povaha světla:
Christian Huygen navrhl, že světlo se šíří ve formě vlny. Tato teorie má však závažný nedostatek. Nedokázala vysvětlit šíření světla ve vakuu. Tento nedostatek odstranil Maxwell, který navrhl, že světlo je elektromagnetické vlnění a pro šíření elektromagnetických vln není zapotřebí žádné hmotné prostředí. Tím byla prokázána vlnová povaha světla.
Vlnová teorie dokázala vysvětlit všechny jevy spojené s šířením světla. Nedokázala však vysvětlit rozložení energie a moderní jevy, jako je fotoelektrický jev, Cromptonův jev atd.
Částicová povaha světla:
Max Planck dokázal, že šíření světla neboli energie probíhá ve formě paketů energie zvaných kvanta. Kvantum světla se nazývá foton, a tím stanovil částicovou povahu světla. Pomocí částicové neboli kvantové povahy záření můžeme vysvětlit jev fotoelektrického jevu a Cromptonova jevu.
Planckova kvantová teorie:
Kvantovou teorii navrhl Max Planck. Podle této teorie není záření ze zdroje vyzařováno spojitě, ale je vyzařováno v balíčcích nebo svazcích energie. Tyto balíčky se nazývají kvanta nebo fotony. Pokud má záření frekvenci ν, má každé kvantum energii, kde h je Planckova konstanta.
Takže energie fotonu = E = hν
Energieje vyzařována nespojitě. To je v rozporu s klasickouteorií, která předpokládá, že emise energie je spojitý proces.
Částicová povaha elektromagnetického záření:
Při interakci záření s hmotou se záření chová, jako by bylo složeno z částic. Tyto částice se nazývají fotony. Každý foton má energii, kteráje dána vztahem
E = hν = hc/λ
Všechny fotony světla určité frekvence (vlnové délky) mají přiřazeno stejné množství energie. Zvýšením intenzity světla se zvýší počet fotonů za sekundu procházejících danou plochou, ale energie každého fotonu bude stejná. Fotony jsou elektricky neutrální a nemají na ně vliv elektrická ani magnetická pole. Fotony se pohybují přímočaře rychlostí světla „c“, ale za určitých podmínek vykazují difrakci.
Moment hybnosti každého fotonu je dán vztahem
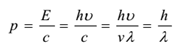
Vlnová délka fotonu se mění s prostředím, proto mají v různých prostředích různérychlosti. Klidová hmotnost fotonu je nulová. Jeho kinetická hmotnost je dána vztahem
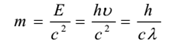
Při srážce fotonu s částicí (například při srážce fotonu s elektronem) se celková energie a hybnost zachovávají. Při srážce se však nemusí zachovat počet fotonů. Foton může být pohlcen nebo může vzniknout nový foton.
Einsteinova fotoelektrická rovnice:
Na základě Planckovy kvantové teorie odvodil Einstein rovnici pro fotoelektrický jev známou jako Einsteinova fotoelektrická rovnice. Einstein předpokládal, že
- Světlo se skládá z fotonů neboli kvant energie, energie v každém fotonu je hν. Kde h je Planckova konstanta a ν je frekvence světla
- Každý dopadající foton se srazí s elektronem uvnitř atomu a předá mu veškerou svou energii.
- Část této energie elektron využije k výstupu z povrchu kovu a zbývající část je kinetická energie, s níž je elektron vyzářen.
- Minimální energie, kterou elektron potřebuje k výstupu z povrchu kovu, se nazývá fotoelektrická pracovní funkce (∅o) kovu.
- Zbývající energie (hν – ∅o) je maximální kinetická energie elektronu, s níž bude fotoelektron vyvržen.
Takto: Maximální kinetická energie elektronu = energie fotonu – pracovní funkce
Nechť „m“ je hmotnost elektronu a vmax je maximální rychlost fotoelektronu, kterou bude vyvržen.

Tato rovnice je známá jako Einsteinova fotoelektrická rovnice
Fotoelektrická pracovní funkce:
Při fotoelektrickém jevu je odstraněn nejvolněji připojený elektron atomu světlocitlivého materiálu. Minimální energie potřebná k uvolnění elektronu z daného povrchu se nazývá fotoelektrická pracovní funkce (∅o) materiálu povrchu. Pracovní funkce je charakteristickou vlastností kovového povrchu.
Matematicky je pracovní funkce dána vztahem
∅o = h νo
Kde νo = prahová frekvence a h =Planckova konstanta.
Vysvětlení existence prahové frekvence na základě Einsteinovy fotoelektrické rovnice:
Pro daný kovový povrch jsou fotoelektrony emitovány pouze tehdy, když je frekvence dopadajícího světla větší nebo rovna určité minimální frekvenci (č)známé jako prahová frekvence. Prahová frekvence je pro různé látky různá,
podle Einsteinovy fotoelektrické rovnice

kde νo = prahová frekvencea h = Planckova konstanta a
ν = frekvence dopadajícího záření
Kinetická energie je vždy nezáporná veličina i.tj. může být buď kladná, nebo nulová, tedy

Z čehož vyplývá, že pro fotoelektrický jev by frekvence dopadajícího záření nebo dopadajícího fotonu měla být rovna nebo větší než prahová frekvence. Přitažlivá síla působící na pravděpodobné fotoelektrony v různých atomech je různá. Proto je prahová frekvence pro různé látky různá.
Vysvětlení vlivu intenzity na základěEinsteinovy fotoelektrické rovnice:
Je-li frekvence dopadajícího světla menší než prahová frekvence,fotoelektrony nejsou emitovány, ať je intenzita dopadajícího světla jakkoli velká.
Počet fotoelektronů emitovaných za sekundu je přímo úměrný intenzitě dopadajícího světla. Fotoelektrický proud je tedy přímoúměrný intenzitě dopadajícího světla. Je-li intenzita světla větší, je počet dopadajících fotonů na povrch větší. V důsledku zvýšeného počtu fotoelektronů se zvyšuje rychlost fotoemise, a tím i síla fotoelektrického proudu. Můžeme tedy konstatovat, že fotoelektrický efekt (proud) je přímo úměrný intenzitě dopadajícího záření.
Vysvětlení možné maximální kinetické energie na základě Einsteinovy fotoelektrické rovnice:
Podle Einsteinovy fotoelektrické rovnice

Kde νo = prahová frekvencea h = Planckova konstanta a
ν = frekvence dopadajícího záření
Tato rovnice neobsahuje člen intenzity, můžeme tedy říci, žemaximální kinetická energie fotoelektronu je nezávislá na intenzitě dopadajícího záření, ale závisí na frekvenci dopadajícího záření. Z této rovnice vyplývá, že maximální kinetická energie elektronu závisí na frekvenci dopadajícího záření. A pokud se frekvence dopadajícího záření zvýší, zvýší se i kinetická energie fotoelektronu.
Vysvětlení okamžitosti fotoelektrického jevu na základě Einsteinovy fotoelektrické rovnice:
Fotoelektrický jev je okamžitý proces. Mezi dopadem světla a emisí fotoelektronů není žádná časová prodleva, jinými slovy, povrch začne emitovat fotoelektrony, jakmile na něj dopadne světlo. Rovněž emise fotoelektronů se zastaví v okamžiku, kdy je dopadající světlo přerušeno.
Pokud na fotoelektrický povrch v tomto okamžiku dopadne záření, celá energie fotonu se jednorázově přenese na jeden elektron. Elektron se tedy vyzáří bez jakékoli časové prodlevy a fotoelektrický jev je okamžitý proces.
Předchozí téma: Další téma: Numerické úlohy o fotoelektrickém jevu
Další téma: Fotoelektrický jev: Numerické úlohy na fotoelektrický jev
