también conocido como fiabilidad entre evaluadores o concordancia
En estadística, la fiabilidad entre evaluadores, el acuerdo entre evaluadores o la concordancia es el grado de acuerdo entre evaluadores. Da una puntuación de cuánta homogeneidad, o consenso, hay en las calificaciones dadas por los jueces.
Los Kappas cubiertos aquí son más apropiados para los datos «nominales». El orden natural en los datos (si existe) es ignorado por estos métodos. Si vas a utilizar estas métricas asegúrate de conocer sus limitaciones.
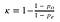
Esto tiene dos partes:
- Calcular la concordancia observada
- Calcular la concordancia por azar
Digamos que estamos tratando con respuestas «sí» y «no» y 2 calificadores. Aquí están las valoraciones:
rater1 =
rater2 =
Convirtiendo estas valoraciones en una matriz de confusión:

Observed agreement = (6 + 1) / 10 = 0.7
Chance agreement = probability of randomly saying yes (P_yes) + probability of randomly saying no (P_no)
P_yes = (6 + 1) / 10 * (6 + 1) / 10 = 0.49
P_no = (1 + 1) / 10 * (1 + 1) / 10 = 0.04
Chance agreement = 0.49 + 0.04 = 0.53
Como el acuerdo observado es mayor que el acuerdo por azar obtendremos un Kappa positivo.
kappa = 1 - (1 - 0.7) / (1 - 0.53) = 0.36
O simplemente utilizar la implementación de sklearn
from sklearn.metrics import cohen_kappa_scorecohen_kappa_score(rater1, rater2)
que devuelve 0,35714.
Interpretación de Kappa

Casos especiales
Acuerdo inferior al azar
rater1 =
rater2 =
cohen_kappa_score(rater1, rater2)
-0.2121
Si todas las valoraciones son iguales y opuestas
Este caso produce de forma fiable un kappa de 0
rater1 = * 10
rater2 = * 10
cohen_kappa_score(rater1, rater2)
0.0
Valoraciones aleatorias
Para las valoraciones aleatorias Kappasigue una distribución normal con una media de aproximadamente cero.
A medida que aumenta el número de valoraciones hay menos variabilidad en el valor de Kappa en la distribución.
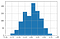
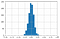
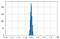
Puede encontrar más detalles aquí
Nótese que el Kappa de Cohen sólo se aplica a 2 calificadores que califican exactamente los mismos ítems.
